你已经训练好一个 Transformer，想用它来生成一些新序列。说到底，基准分数上升和损失曲线下降，只是衡量模型在实际应用中能否产生有趣结果的代理指标！从历史上看，你可以在完全不接触推理的情况下，对 Transformer 进行大量研究——LLM 损失、多项选择基准测试都可以在没有合适的 KV 缓存或生成循环实现的情况下高效运行。这意味着，尤其是在研究代码库中，推理代码路径上通常有很多容易摘取的低垂果实。

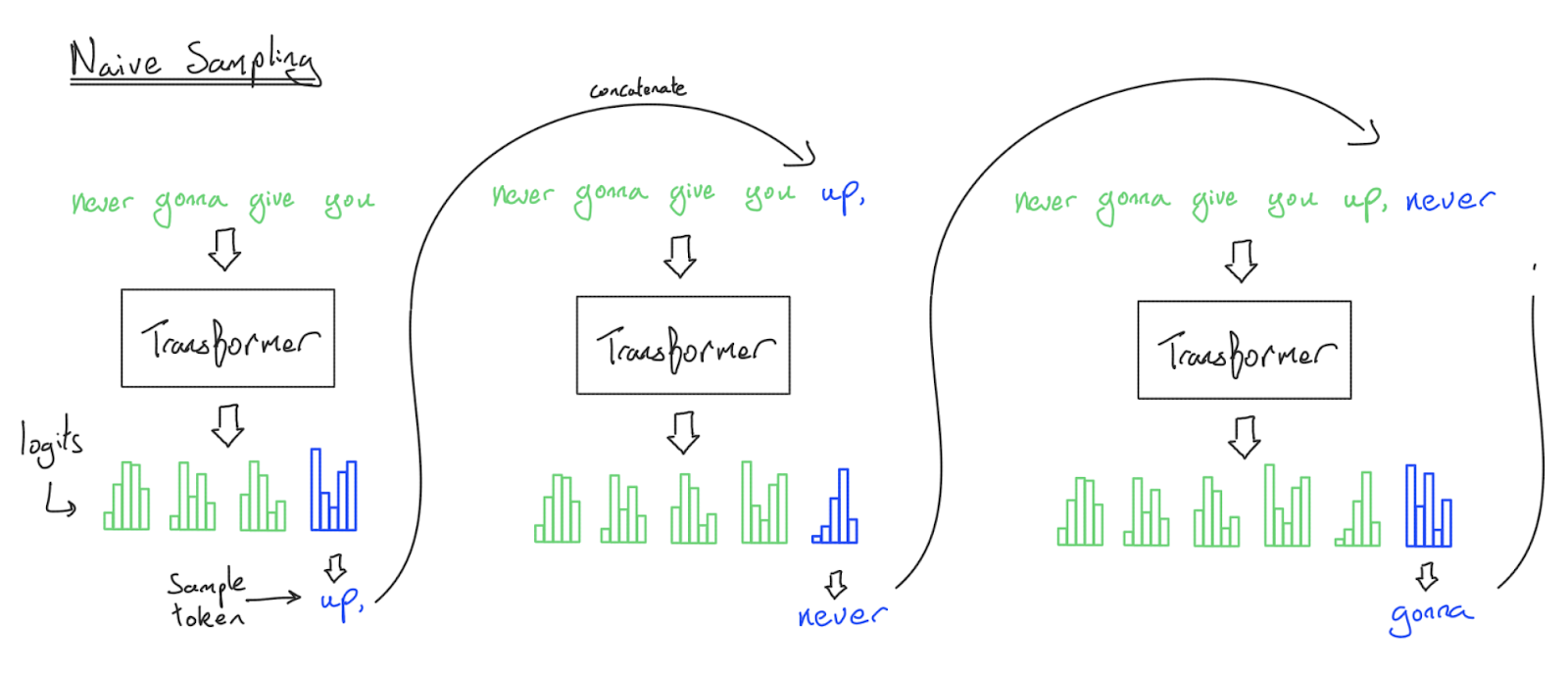
采样在概念上很简单。我们输入一个序列，我们钟爱的 Transformer 就会输出 $\log p ({next token}_{i} | previous tokens)$ ，即所有可能的下一个词元的对数概率。我们可以从这个分布中采样，得到一个新的词元。将这个词元追加到序列中，重复这个过程，我们就得到了一个作为提示延续的词元序列。

图：从 Transformer 进行朴素采样。蓝色的 logits 为我们提供了下一个词元的分布，我们可以从中采样。注意，每一步都会重新处理整个前缀，导致算法的运行时间为 \Theta(n^2)。

我们刚刚描述了 Transformer 采样的朴素实现，虽然它能工作，但我们在实践中从不这样做，因为每次生成一个词元时，我们都在重新处理整个序列。这个算法在 FFW 上的复杂度是 $O (n^{2})$ ，在注意力机制上的复杂度是 $O (n^{3})$ ，才能生成 $n$ 个词元！

我们如何避免这种情况？ 事实证明，我们不必每次都进行完整的正向传播，而是可以保存每次正向传播的一些中间激活值，从而避免重新处理之前的词元。具体来说，由于在点积注意力中，一个给定的词元只关注之前的词元，我们可以简单地将每个词元的键（key）和值（value）投影写入一个名为 KV 缓存 的新数据结构中。一旦我们为过去的词元保存了这些键/值投影，未来的词元就可以简单地计算它们的 $q_{i} \cdot k_{j}$ 乘积，而无需对早期的词元执行任何新的 FLOPs。太棒了！

考虑到这一点，推理有两个关键部分：

预填充：给定一个长提示，我们同时处理提示中的所有词元，并将生成的激活值（特别是键值投影）保存在一个 “KV 缓存” 中。我们还保存最后一个词元的 logits。
生成：给定一个 KV 缓存和前一个 logits，我们从 logits 中增量地采样一个词元，将该词元反馈给 Transformer，并为下一步生成一组新的 logits。我们还将新词元的 KV 激活值附加到 KV 缓存中。我们重复这个过程，直到遇到一个特殊的 <EOS> 词元或达到某个最大长度限制。

下图是使用 KV 缓存进行采样的示意图：

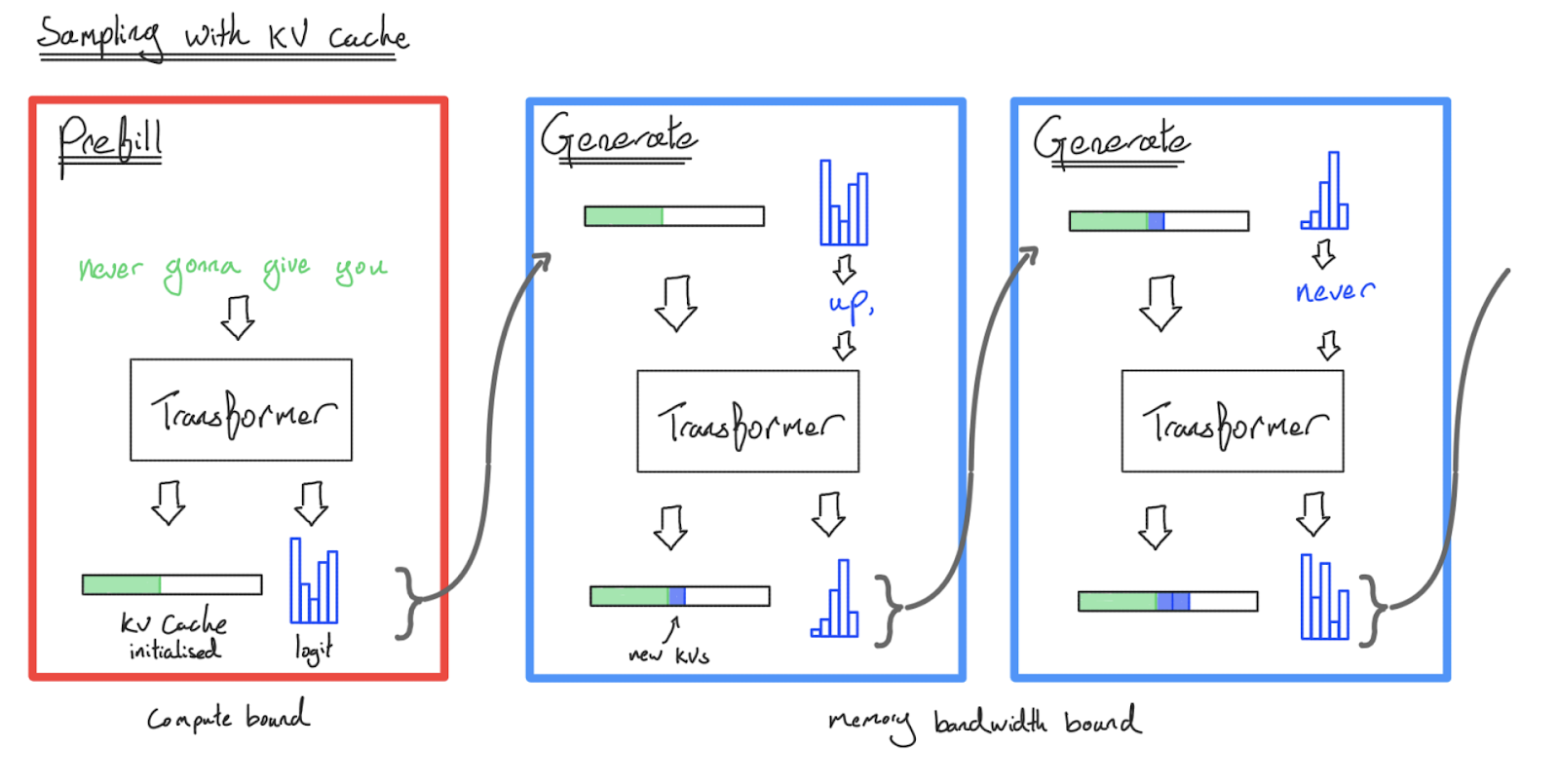
图：使用 KV 缓存进行高效 Transformer 采样的示意图。**预填充**处理我们的提示，并将每个词元的键值激活值保存在缓存中。生成接收这个缓存（以及最后一个词元的 logits），采样一个新词元，并将该新词元传递给模型，模型会关注 KV 缓存，并将新词元的键值投影保存回缓存中。在 MLP 块中，这是一个 O(n) 算法。

通过使用 KV 缓存进行采样，我们将生成 n 个词元的时间复杂度在 FFW 上降低到 $O (n)$ ，在注意力上降低到 $O (n^{2})$ ，因为我们从不重新处理之前的词元。然而，生成一个序列仍然需要多次正向传播——当你查询 Gemini 或 ChatGPT 并看到结果以流式方式返回时，发生的就是这个过程。每个词元（通常）都是对一个巨大模型的独立（但部分缓存的）Transformer 调用。

我们很快就会看到，预填充和生成是两种截然不同的任务——Transformer 推理实际上是伪装成一个任务的两个任务！与训练相比，KV 缓存也是一个新颖且重要的复杂性来源。

我们究竟想优化什么？

在继续之前，值得强调推理中一个全新的方面：延迟。在训练期间，我们只关心吞吐量（每秒处理的总词元数），而在推理期间，我们必须关心生成词元的速度（包括首词元时间（TTFT）和每词元延迟）。例如：

用于评估和数据生成的离线批量推理只关心推理的批量成本，而忽略单个样本的延迟。
聊天界面/流式任务需要在低 TTFT 的同时，以低成本大规模运行，并且生成词元的速度要快到超过人类的阅读速度。
边缘推理（例如，在你笔记本电脑上运行的 llama.cpp）只需要在尽可能低的延迟下一次服务一个用户，且可能面临严格的硬件限制。

最大化硬件利用率仍然至关重要，有助于降低成本和 TTFT，但与训练不同，它并不一定在所有情况下都能转化为更好的单个用户体验。在加速器、系统和模型架构层面的许多优化，都是在延迟、吞吐量、上下文长度甚至模型质量之间进行权衡。

更细粒度地审视 Transformer

到目前为止，我们主要将 Transformer 视为一堆前馈块。虽然从 FLOPs 和内存的角度来看，这通常是合理的，但这不足以正确地为推理建模。在本节中，你会注意到一件事，那就是推理远不如训练那样宽容。我们通常拥有的 FLOPs 要少得多，批处理的机会也更少，而且对延迟的敏感度要高得多。KV 缓存也极大地复杂化了推理。正如我们在第 4 部分中看到的，Transformer 正向传播的主要组成部分是：

一系列线性操作，包括 MLP (W_{in}, W_{out}) 和注意力 QKV 投影及输出投影 (W_Q, W_K, W_V, 和 W_O)。这些都涉及从 HBM 读取参数和一批激活值，执行一些 FLOPs，然后将结果写回 HBM。
点积注意力。我们需要从 HBM 读取一批键值投影和一批查询激活值，进行一些内积和 softmax 操作，然后将注意力结果写回 HBM。
其他所有操作，包括应用层归一化、激活函数、词元采样、更新 KV 缓存和位置嵌入。这些操作确实会消耗一些 FLOPs，但与上述操作相比，它们要么占主导地位，要么被融合到上述操作中。

在接下来的几节中，我们将在预填充和生成的背景下审视这些操作，并探究什么可能成为我们性能的瓶颈。在单个加速器内，我们是受计算限制还是受内存限制？我们想强调的是，对于预填充和生成，答案将会有多大的不同。

线性操作：瓶颈何在？

我们所有的线性操作在概念上都是相同的，无论它们位于 MLP 块还是注意力模块中。它们的算术强度取决于批量大小。我们在第 1 节中做过这个数学计算，但值得重复一遍。让我们看一个 \text{bf16[B, D]} 批次与一个 \text{bf16[D, F]} 矩阵的单次矩阵乘法。这可能是大的 MLP 块（W_\text{in} 或 W_\text{out}）或较小的注意力投影之一（W_Q, W_K, W_V, W_O）。要进行这次矩阵乘法，我们需要将这两个数组从 HBM 加载到 MXU 中，进行乘法运算，然后将结果写回 HBM。和之前一样，我们有：

T_{math} = \frac{Computation FLOPs}{Accelerator FLOPs/s} = \frac{2 B D F}{Accelerator FLOPs/s}

T_{comms} = \frac{Communication Bytes}{Bandwidth Bytes/s} = \frac{2 B D + 2 F D + 2 B F}{Bandwidth Bytes/s}

TPU 或 GPU 可以在进行计算的同时加载数据，从而重叠这些操作，因此要达到计算密集型，我们需要 $T_{math} \geq T_{comms}$ ，或者：

\frac{2 B D F}{2 B D + 2 D F + 2 B F} \geq \frac{Accelerator FLOPs/s}{Bandwidth Bytes/s} \underset{TPU v5e}{=} \frac{1.97 E + 14}{8.20 E + 11} = 240

其中右侧是我们硬件的算术强度。现在让我们假设 D 和 F 与 B 相比非常大（通常我们的批次最多为 500，且 D 和 F > 10k），我们可以通过 \small{2BD + 2DF + 2BF \approxeq 2DF} 这个事实来简化分母，从而得到

\begin{array}{r} \frac{2 B D F}{2 B D + 2 D F + 2 B F} ≊ \frac{2 B D F}{2 D F} \geq \frac{Accelerator FLOPs/s}{Bandwidth Bytes/s} \\ \underset{TPU v5e}{=} \frac{1.97 E + 14}{8.20 E + 11} ⟹ B \geq 240 = B_{crit} \end{array}

如果我们对权重进行量化，或使用较低精度的 FLOPs 进行矩阵乘法，这个临界批量大小会发生变化。例如，如果我们将权重化为 int8 或 fp8，B_\text{crit} 会减少 2 倍。如果我们在 int8 或 fp8 中进行 FLOPs 计算，B_\text{crit} 会增加 2 倍。因此，如果我们设 \beta = \text{bits per param} / \text{bits per activation} 且 \alpha_\text{hbm} = C / W_\text{hbm}，我们的临界批量大小实际上是 B_\text{crit} = \beta \alpha_\text{hbm}。

要点： Transformer 矩阵乘法是计算密集型的，当且仅当每个副本的词元批量大小大于 B_\text{crit} = C / W_\text{hbm} \cdot (\text{bits per param} / \text{bits per activation}) = \beta \cdot \alpha_\text{hbm}。对于 TPU v5e 上的 bf16 激活，这个值是 240 个词元。对于 H100，大约是 280 个词元。

在训练期间，我们所有的矩阵乘法都具有高强度，因为我们在一个非常大的批次上重用相同的权重。这种高算术强度也延续到了预填充阶段，因为用户提示通常有数百甚至数千个词元长。 正如我们之前看到的，TPUv5e 的硬件算术强度是 240，所以如果一个长于 240 个词元的序列以 bf16 精度输入到运行在此硬件上的密集模型中，我们预计会是计算密集型的，一切正常。比这更短的提示理论上可以批处理在一起以实现更高的利用率，但这通常没有必要。

要点： 在预填充期间，所有矩阵乘法基本上总是计算密集型的。因此，只需最大化硬件利用率或 MFU（模型 FLOPs 利用率）就足以最大化每芯片吞吐量（成本）和延迟（以 TTFT 的形式）。除非提示非常短，否则在每个提示级别进行批处理只会增加延迟，而对预填充吞吐量的提升很小。

然而，在生成期间，对于每个请求，我们一次只能进行一个词元的正向传播，因为步骤之间存在顺序依赖！因此，我们只能（容易地）通过将多个请求批处理在一起，在批次维度上并行化，来实现良好的利用率。我们稍后会更多地讨论这一点，但实际上，在不影响延迟的情况下将许多并发请求批处理在一起是很困难的。因此，用生成来饱和硬件的 FLOPs 要困难得多。

要点： 在生成期间，总词元批量大小必须大于 B_{\text{crit}}，才能在线性/前馈操作上达到计算密集型（对于 TPU v5e 上的 bf16 参数，该值为 240）。因为生成是串行地、逐词元进行的，这要求我们将多个请求批处理在一起，这很困难！

值得注意的是这个数字有多大！ 生成批量大小为 240 意味着 240 个并发请求同时生成，对于密集模型来说，需要 240 个独立的 KV 缓存。这意味着在实践中很难实现，除非在某些批量推理场景中。相比之下，在预填充期间处理超过 240 个词元是相当常规的，尽管随着稀疏性的增加需要一些注意。

请注意，这个确切的数字会因量化类型和硬件而异。 加速器通常可以在较低精度下提供更多的算力。例如，如果我们有 int8 参数但在 bf16 中进行计算，临界批量大小会降至 120。使用 int8 激活和 int8 参数，它又会跳回到 240，因为 TPUv5e 可以提供 400 TOPs/s 的 int8 x int8 算力。

注意力机制呢？

当我们审视点积注意力操作时，事情变得更加复杂，特别是我们必须考虑 KV 缓存。让我们只看一个具有纯多头注意力的注意力头。在一次 Flash Attention 融合中，我们我们在这里做了相当多的简化，忽略了应用 softmax、掩码等操作中的非矩阵乘法 FLOPs。它们应该与计算或 HBM 读取重叠，但在某些 TPU 代上实现起来可能不简单。这些细节不会改变主要信息，即 KV 缓存通常是受内存限制的。：

从 HBM 读取形状为 Q 的 \text{bf16[B, T, D]} 激活。
从 HBM 读取 KV 缓存，它是一对 \text{bf16[B, S, D]} 张量。
在 $Q K$ 矩阵乘法中执行 2BSTD FLOPs。使用 Flash Attention，我们不需要将 \text{bf16[B, S, T]} 注意力矩阵写回 HBM。
在注意力 $A V$ 矩阵乘法中执行 2BSTD。
将得到的 \text{bf16[B, T, D]} 张量写回 HBM。

综上所述，我们得到：

Multiheaded Attention Arithmetic Intensity = \frac{4 B S T D}{4 B S D + 4 B T D} = \frac{S T}{S + T}

对于预填充，S=T 因为我们正在做自注意力，所以这简化为 T^2 / 2T = T / 2。这很好，因为这意味着预填充期间注意力的算术强度是 \Theta(T)。这意味着注意力很容易达到计算密集型。只要我们的序列长度足够大，就没问题！

但是由于生成的序列维度很小，并且 B 和 D 维度相互抵消，我们可以做如下近似：

S ≫ T = 1 ⟹ \frac{S T}{S + T} \approx 1

这很糟糕，因为它意味着我们无法做任何事情来提高生成期间注意力的算术强度。我们在加载一个巨大的 KV 缓存的同时，只做了极少量的 FLOPs。所以我们在注意力计算期间基本上总是受内存带宽限制的！

要点：在预填充期间，对于任何合理的序列长度（大约 \gt 480 个词元），注意力通常是计算密集型的；而在生成期间，我们的算术强度很低且为常数，所以我们总是受内存带宽限制。

从概念上讲，这是为什么？ 主要原因是，我们在模型的线性部分是计算密集型的，因为参数（内存带宽密集型组件）被许多批次项重用。然而，每个批次项都有自己的 KV 缓存，所以更大的批量大小意味着更多的 KV 缓存。除非架构被大幅调整，否则我们在这里几乎总是受内存限制。

这也意味着，一旦参数内存变得与 KV 缓存内存相当，通过增加批量大小来提高吞吐量将获得递减的回报。回报递减的程度取决于单个序列的参数与 KV 缓存字节的比率，即大约 2DF / SHK。由于 HK\approx D，这大致取决于 F 与序列长度 S 的比率。这也取决于使 KV 缓存变小的架构修改（我们稍后会详细说明）。

LLM 延迟和吞吐量的理论估算

通过这个数学计算，我们可以得到优化时应该追求的步长时间的相当好的界限。（注意：如果说我们希望读者从本章中学到一件事，那就是接下来的内容）。 对于生成期间的小批量大小（这很常见），我们可以通过假设我们在注意力和 MLP 块中都受内存带宽限制，来得到每步延迟的下界：

Theoretical Min Step Time = \frac{Batch Size \times KV Cache Size + Parameter Size}{Total Memory Bandwidth}

同样，对于吞吐量：

Theoretical Max Tokens/s = \frac{Batch Size \times Total Memory Bandwidth}{Batch Size \times KV Cache Size + Parameter Size}

最终，随着批量大小的增长，FLOPs 开始主导参数加载，因此在实践中我们有更通用的方程：

\begin{array}{r} (1) & Theoretical Step Time (General) = \underset{Attention (always bandwidth-bound)}{\underset{⏟}{\frac{Batch Size \times KV Cache Size}{Total Memory Bandwidth}}} + \underset{MLP (can be compute-bound)}{\underset{⏟}{max (\frac{2 \times Batch Size \times Parameter Count}{Total FLOPs/s}, \frac{Parameter Size}{Total Memory Bandwidth})}} \end{array}

其中注意力部分（左）从不是计算密集型的，因此不需要 FLOPs Roofline。这些对于进行粗略计算相当有用，例如

小测验： 假设我们想在一个 4x4 的 TPU v5e 切片上，使用 int8 参数和 bf16 FLOPs，对一个 30B 参数的密集模型进行一个生成步骤，批量大小为 4 个词元，上下文长度为 8192，每个词元的 KV 缓存为 100 kB。这个操作的延迟的合理下界是多少？如果我们想采样一批 256 个词元呢？

点击此处查看答案。

答案： 在 int8 中，我们的参数将使用 30e9 字节，根据给定的规格，我们的 KV 缓存每个将使用 100e3 * 8192 = 819MB。我们有 16 个芯片，每个芯片的带宽为 8.1e11 字节/秒，bf16 FLOPs/秒为 1.97e14。根据上述方程，由于我们的批量大小很小，我们预计步长时间至少为 (4 * 819e6 + 30e9) / (16 * 8.1e11) = 2.5 ms。对于 256 个词元，我们的 MLP 块将远超计算密集型区域，所以步长时间大约为 (256 * 819e6) / (16 * 8.1e11) + (2 * 256 * 30e9) / (16 * 1.97e14) = 21ms。

正如你所见，这里在吞吐量和延迟之间存在明显的权衡。小批量速度快，但硬件利用率不高。大批量速度慢，但效率高。以下是为一些旧的 PaLM 模型计算的延迟-吞吐量帕累托前沿（来自 ESTI 论文）：

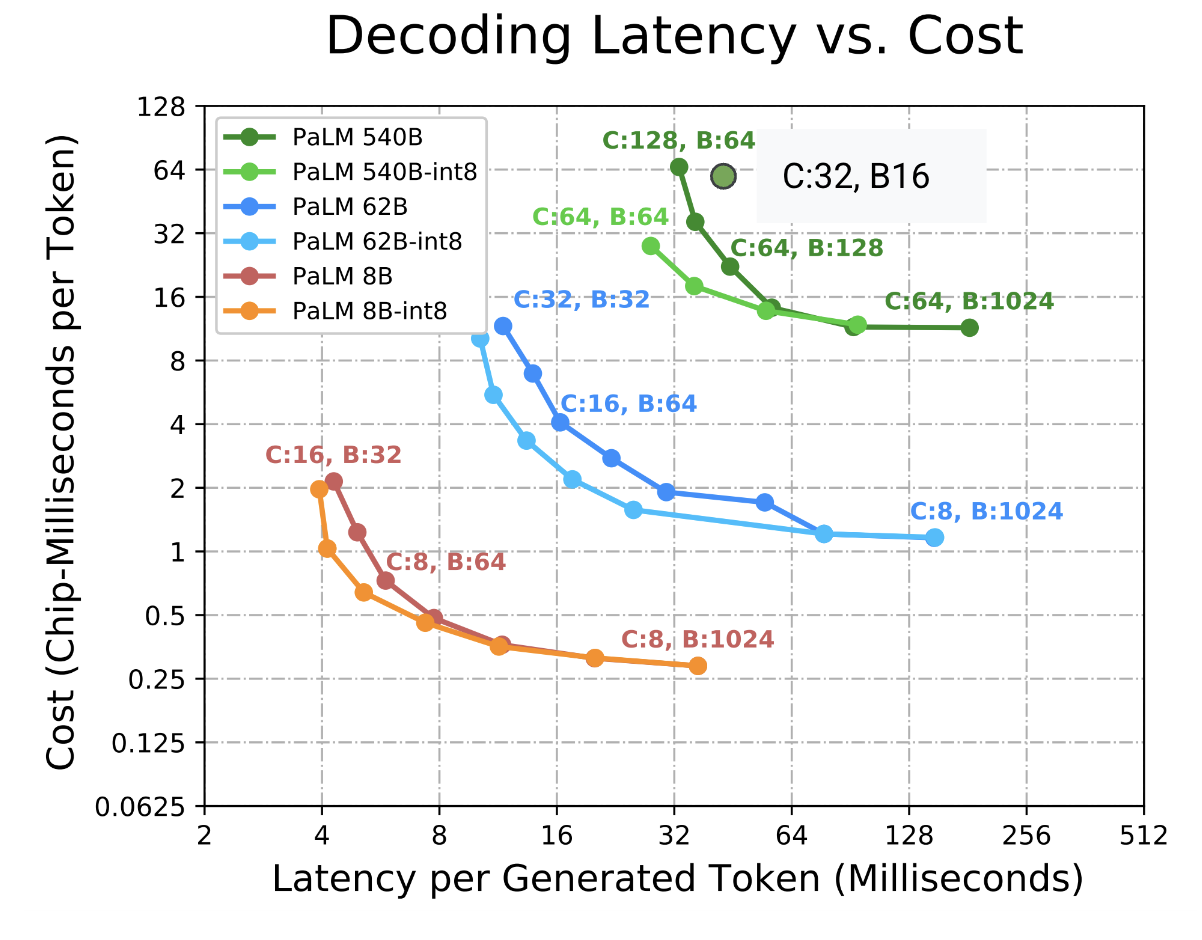
图：几个 PaLM 模型的成本（即吞吐量）与延迟的帕累托前沿。注意芯片数量（C）和批量大小（B）如何让你在帕累托前沿上移动，除了绿点（PaLM 540B 的 C:32 B:16），那里的可用内存阻止了设置支持一个好的批量大小，并导致吞吐量受损。注意吞吐量通常在批量大小 240 之后趋于平缓。int8 权重提供了更好的延迟-吞吐量帕累托最优，但最大吞吐量没有更好。

我们不仅通过批量大小作为调节旋钮来权衡延迟和吞吐量，如果我们发现自己受 HBM 限制，我们也可能更喜欢更大的拓扑结构而不是更小的，以便容纳更大的批次。下一节将更详细地探讨这一点。

要点： 如果你关心生成吞吐量，请使用尽可能大的每芯片批量大小。任何高于 TPU 算术强度（B_\text{crit}，通常为 120 或 240）的每芯片批量大小都将最大化吞吐量。你可能需要增加你的拓扑结构来实现这一点。较小的批量大小将允许你以牺牲吞吐量为代价来改善延迟。

从硬件的角度来看，这有一些需要注意的地方。点击这里查看一些细节。

这一切都相当理论化。在实践中，我们通常不会看到一个尖锐的Roofline，原因有几个：

我们关于 HBM 读取将与 FLOPs 完全重叠的假设是不现实的，因为我们的编译器（XLA）并非完美无缺。
对于分片模型，XLA 也常常无法有效地将我们模型分片矩阵乘法的 ICI 通信与 FLOPs 本身重叠，所以我们经常在线性操作上开始遭受延迟损失，超过 $BS = 32$ 。
大于理论Roofline的批量大小仍然会看到一些吞吐量的改善，因为重叠不完美，但这只是一个很好的启发式方法。

内存方面呢？

我们花了一些时间研究带宽和 FLOPs，但没有研究内存。由于我们新的数据结构——KV 缓存，推理时的内存情况看起来大不相同。在本节中，我们将选择一个真实模型（LLaMA 2-13B）来展示情况有多么不同：

超参数	值
L (num_layers)	40
D (d_model)	5,120
F (ffw_dimension)	13,824
N (num_heads)	40
K (num_kv_heads)	40
H (qkv_dim)	128
V (num_embeddings)	32,000

在推理期间什么在占用内存？嗯，很明显，是我们的参数。计算这些，我们有：

参数	公式	大小 (字节)
FFW 参数	d_model² x ffw_multiplier x 3 (用于 gelu + 输出投影) x n_layers	5,120 x 5,120 x 2.7 x 3 x 40 = 8.5e9
词汇表参数	2 (输入和输出嵌入) x n_embeddings x d_model	2 x 32,000 x 5,120 = 0.3e9
注意力参数	[2 (q 和输出) x d_model x n_heads x d_qkv + 2 (用于 k 和 v) x d_model x n_kv_heads x d_qkv] x n_layers	(2 x 5,120 x 40 x 128 + 2 x 5,120 x 40 x 128) x 40 = 4.2e9

将这些参数加起来，我们得到 8.5e9 + 4.2e9 + 0.3e9 = 13e9 总参数，正如预期的那样。正如我们在前几节中看到的，在训练期间，我们可能会将参数存储在 bfloat16 中，并将优化器状态存储在 float32 中。这可能会使用大约 100GB 的内存。与我们的梯度检查点相比，这相形见绌，后者可能使用数 TB。

推理有何不同？ 在推理期间，我们存储一份参数，比如以 bfloat16 格式。这会占用 26GB——实际上，通过量化，我们通常可以做得更好。没有优化器状态或梯度需要跟踪。因为我们不进行检查点（为反向传播保留激活），我们的激活占用空间对于预填充特别要感谢 Flash Attention，它避免了将我们的注意力矩阵实例化和生成来说都是微不足道的。如果我们预填充 8k 个词元，单个激活仅使用大约 8,192 x 5,120 x 2 字节 = 80MB 的内存。更长的预填充可以分解为许多更小的正向传播，因此对于更长的上下文也不是问题。生成使用的词元甚至更少，所以激活可以忽略不计。

主要区别在于 KV 缓存。这些是所有过去词元的键和值投影，其大小仅受最大允许序列长度的限制。对于 $T$ 个词元的总大小是

KV cache size = 2 \cdot bytes per float \cdot H \cdot K \cdot L \cdot T

其中 $H$ 是每个头的维度， $K$ 是 KV 头的数量， $L$ 是层数，2 来自于同时存储键和值。

即使批量大小和上下文长度适中，这个值也可能迅速变得非常大。对于 LLaMA-13B，一个 8192 序列在 bf16 下的 KV 缓存是

8192 (T) \times 40 (K) \times 128 (H) \times 40 (L) \times 2 (bytes) \times 2 = 6.7 GB

仅仅 4 个这样的缓存就超过了我们参数的内存使用量！ 需要明确的是，LLaMA 2 并未针对较长上下文的 KV 缓存大小进行优化（情况并非总是这么糟，因为通常 K 要小得多，如 LLaMA-3 中），但这仍然具有说明性。我们在内存或延迟估算中不能忽略这些。

为 LLaMA 2-13B 的吞吐量和延迟建模

让我们看看，如果我们尝试在 8 个 TPU v5e 上，以不同的批量大小完美高效地执行生成，直到达到之前为最大理论吞吐量推导出的临界批量大小（240），会发生什么。

批量大小	1	8	16	32	64	240
KV 缓存内存 (GiB)	6.7	53.6	107.2	214.4	428.8	1608
总内存 (GiB)	32.7	79.6	133.2	240.4	454.8	1634
理论步长时间 (ms)	4.98	12.13	20.30	36.65	69.33	249.09
理论吞吐量 (词元/秒)	200.61	659.30	787.99	873.21	923.13	963.53

8 个 TPU v5e 给了我们 128GiB 的 HBM，6.5TiB/s 的 HBM 带宽（每个 0.82TiB/s）和 1600TF/s 的计算能力。

对于这个模型，增加批量大小确实能带来更好的吞吐量，但我们很快就会遇到收益递减的问题。当批量大小超过 16 时，我们就会出现内存不足（OOM），并且需要数量级更多的内存才能接近 240。更大的拓扑结构可以改善延迟，但我们在每个芯片的吞吐量上遇到了瓶颈。

假设我们保持总参数数量不变，但神奇地将 KV 缓存缩小 5 倍（比如说，使用 1:5 的 GMQA，这意味着我们有 8 个 KV 头共享给 40 个 Q 头——详见下一节）。

批量大小	1	8	16	32	64	240
KV 缓存内存 (GiB)	1.34	10.72	21.44	42.88	85.76	321.6
总内存 (GiB)	27.34	36.72	47.44	68.88	111.76	347.6
理论步长时间 (ms)	4.17	5.60	7.23	10.50	17.04	52.99
理论吞吐量 (词元/秒)	239.94	1,429.19	2,212.48	3,047.62	3,756.62	4,529.34

使用更小的 KV 缓存，我们仍然会遇到收益递减的问题，但理论上每个芯片的吞吐量会持续扩展到批量大小为 240。我们可以容纳更大的批次，达到 64，并且在所有批量大小下，延迟也始终更好。延迟、最大吞吐量和最大批量大小都得到了显著改善！事实上，后来的 LLaMA 版本就使用了这个确切的优化——LLaMA-3 8B 有 32 个查询头和 8 个 KV 头（来源）。

要点： 除了参数，KV 缓存的大小对模型的最终推理性能有很大影响。我们需要通过架构决策和运行时优化的结合来控制它。

提升生成吞吐量和延迟的技巧

自最初的 Attention is All You Need 论文以来，已经发展出许多技术来提高模型的效率，通常特别针对 KV 缓存。总的来说，一个更小的 KV 缓存使得在不损害延迟的情况下更容易增加生成步骤的批量大小和上下文长度，并且让围绕 Transformer 的系统（如请求缓存）工作起来更容易。忽略对质量的影响，我们可能会看到：

分组多查询注意力（又名 GMQA, GQA）： 我们可以减少 KV 头的数量，并在注意力机制中与许多 Q 头共享它们。在极端情况下，可以在所有 Q 头之间共享一个 KV 头。这比纯 MHA 将 KV 缓存减少了 Q:KV 的比率倍，并且已经观察到模型的性能对这种变化相对不敏感。

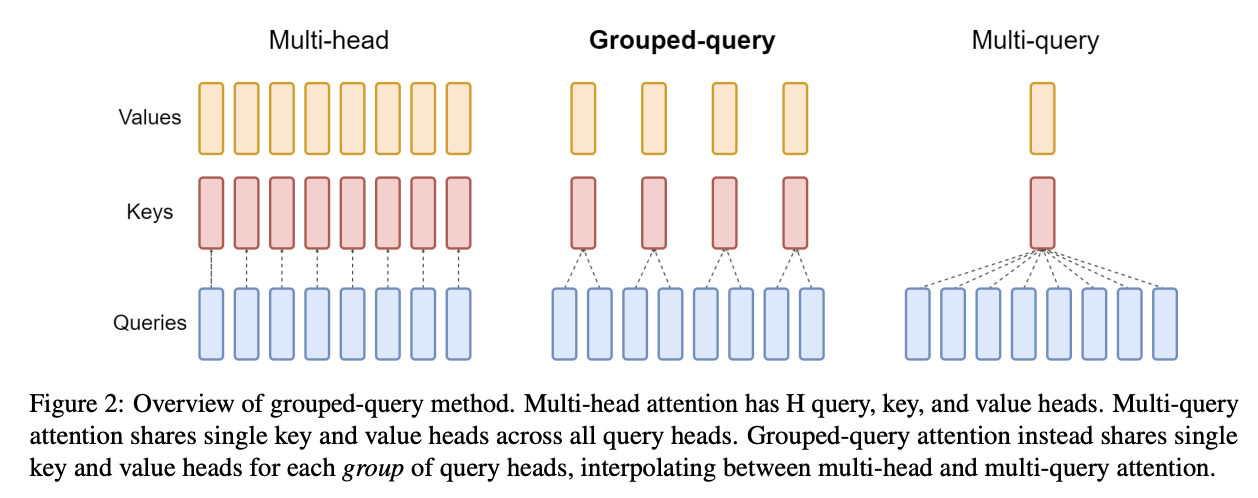
这也有效地增加了注意力计算的算术强度（参见第 4 节中的问题 4）。

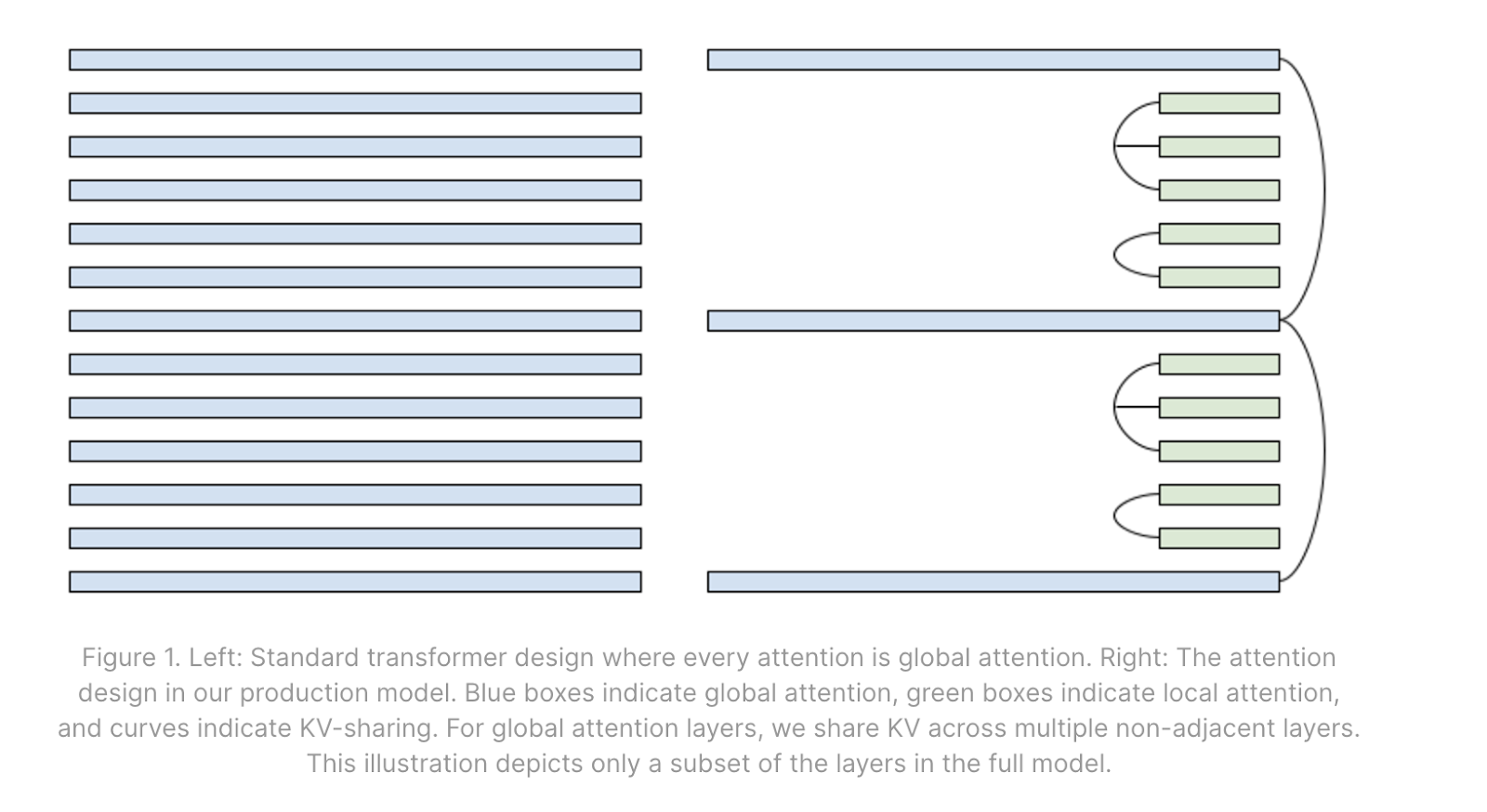
混合一些局部注意力层： 局部注意力将上下文限制在一个小到中等大小的最大长度内。在训练和预填充时，这涉及到将注意力矩阵掩码为一个对角条带而不是一个三角形。这有效地限制了局部层的 KV 缓存的最大长度。通过在模型中混合一些局部层和一些全局层，当上下文长度超过局部窗口时，KV 缓存的大小会大大减小。

跨层共享 KV： 模型可以学习以某种模式在不同层之间共享相同的 KV 缓存。虽然这确实减小了 KV 缓存的大小，并在增加批量大小、缓存、离线存储等方面提供了好处，但共享的 KV 缓存可能需要多次从 HBM 读取，因此不一定能改善步长时间。

**左图：**多层纯全局注意力。**右图：**一个全局/局部交错模式并与相邻层共享的示例。来源：Character.ai 博客。

量化： 推理通常对参数和 KV 的精度不太敏感。通过量化参数和 KV 缓存（例如，量化到 int8、int4、fp8 等），我们可以在两者上节省内存带宽，减少达到计算Roofline所需的批量大小，并节省内存以运行更大的批量。量化还有一个额外的好处，即使模型没有在训练时使用量化，也通常可以在训练后应用。

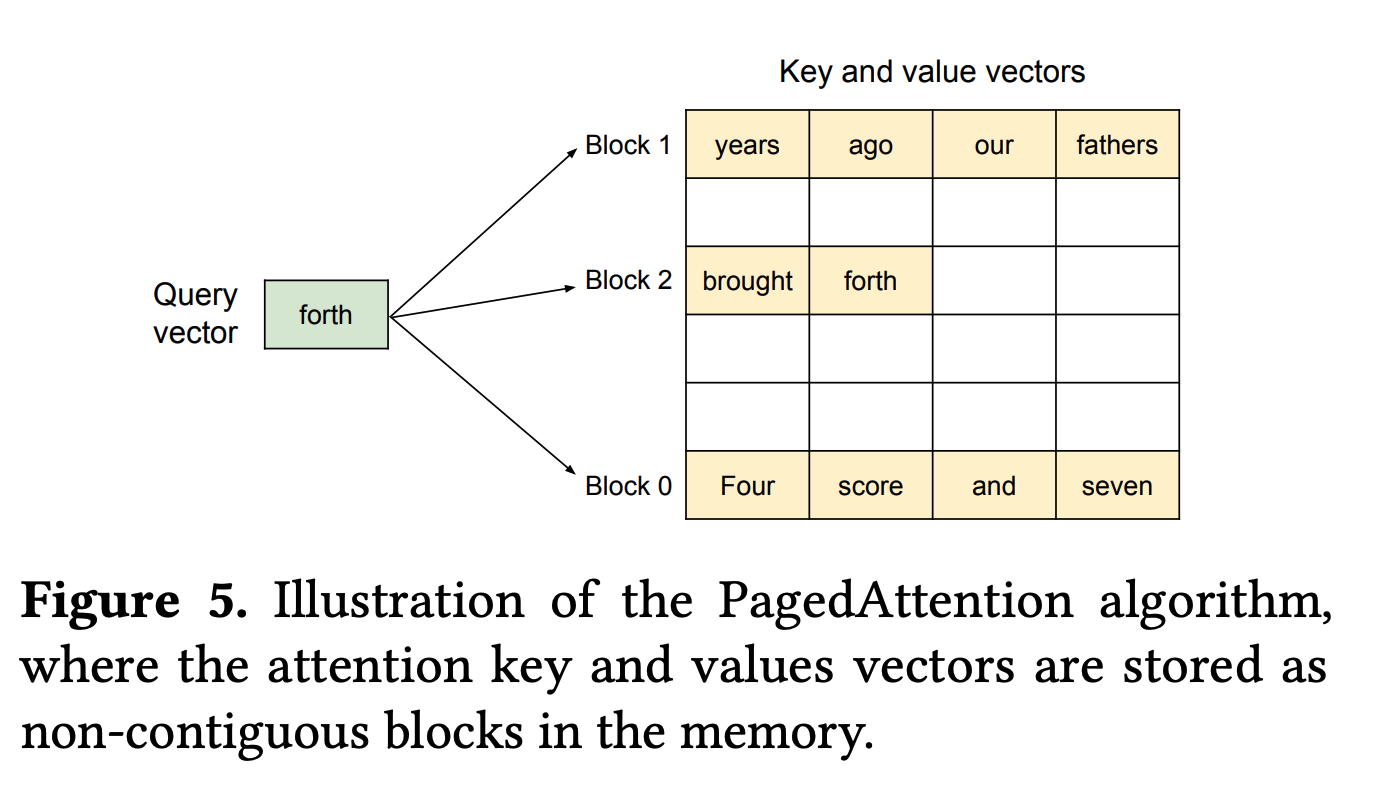
使用非规则 HBM 读取和 Paged Attention： 在上面的计算中，我们为每个 KV 缓存分配了 8k 的上下文，但通常没有必要从内存中读取整个 KV 缓存——请求的长度分布范围很广，并不总是使用模型的最大上下文，所以我们通常可以实现只读取 KV 缓存非填充部分的内核（例如 Flash Attention 变体）。

Paged Attention 是对此的改进，它将 KV 缓存存储在类似操作系统的页表中，并且基本上完全避免了对 KV 缓存的填充。这增加了很多复杂性，但意味着每个批次只使用它需要的内存量。这是一个运行时优化，所以它同样与架构无关。

图：在生成过程中，一个词元（forth）关注多个 KV 缓存块/页。通过对 KV 缓存进行分页，我们避免了加载或存储超出我们需要的内存。引自 PagedAttention 论文。

宏观视角： 总而言之，这些 KV 缓存优化可以将 KV 缓存大小与标准的 MHA Transformer 相比减少一个数量级以上。这可能导致 Transformer 的总成本提高一个数量级。

在多个加速器上分布推理

到目前为止，我们都只是泛泛地谈论如何扩展到单个芯片之外。继第 5 节之后，让我们探讨一下可用的不同策略及其权衡。和往常一样，我们将分别考察预填充和生成。

预填充

从Roofline的角度来看，预填充与训练几乎相同，并且几乎所有相同的技术和权衡都适用——模型（Megatron）并行性、序列分片（对于足够长的上下文）、流水线，甚至 FSDP 都是可行的！你只需要保留 KV，以便稍后进行生成。与训练一样，增加芯片数量可以让我们获得更多的 FLOPs/s（可能降低 TTFT），但会增加通信开销（可能降低每个芯片的吞吐量）。

分片预填充的一般规则： 这里有一套关于预填充的一般规则。我们将假设我们只对单个序列进行预填充（没有批次维度）：

模型分片： 我们通常首先进行一定程度的模型并行性，直到我们受 ICI 限制。正如我们在第 5 节中看到的，对于 1 个轴，这大约是 F / 2200（通常是 4-8 路分片）。
序列并行性： 除此之外，我们进行序列并行性（类似于数据并行性，但在序列维度上进行分片）。虽然序列并行性在注意力中引入了一些额外的通信，但在较长的上下文中，这通常相当小。与训练一样，我们可以重叠通信和计算（分别使用集体矩阵乘法用于 Megatron 和环形注意力）。

要点： 在预填充期间，几乎任何在训练期间可行的分片策略都可以正常工作。先进行模型并行性直到达到 ICI 边界，然后进行序列并行性。

生成

生成比预填充要复杂得多。一方面，很难获得大的批量大小，因为我们需要将许多请求批处理在一起。延迟目标更低。这些因素共同意味着我们通常更受内存限制，对通信开销更敏感，这限制了我们的分片策略：

FSDP 是不可能的： 由于我们在从 HBM 加载参数和 KV 缓存到 MXU 的过程中受内存限制，我们不想通过比 HBM 慢几个数量级的 ICI 来移动它们。我们希望移动激活而不是权重。 这意味着类似 FSDP 的方法通常对于生成是完全不可行的。训练后不小心保留它是导致数量级性能下降的一个简单而常见的方式
没有理由进行数据并行性： 纯数据并行性没有帮助，因为它复制了我们的参数，并且无助于我们更快地加载参数。你最好启动多个模型的副本。我们的意思是，以较小的批量大小启动多个带有模型副本的服务器。模型级别的数据并行性严格来说更差。
没有序列 = 没有序列分片。 祝你好运进行序列分片。

这主要给我们留下了用于密集模型生成的模型分片变体。与预填充一样，我们能做的最简单的事情就是简单的模型并行性（激活完全复制，MLP 的权重在隐藏维度上完全分片），直到 4-8 路时我们受 ICI 限制。然而，由于我们经常受内存带宽限制，我们实际上可以超越这个限制来提高延迟！

关于生成 ICI 边界的说明： 在训练期间，我们希望是计算密集型的，所以我们的Roofline关注的是 ICI 通信时间何时超过 FLOPs 时间。然而，在生成期间，如果我们受参数加载的内存带宽限制，我们可以将模型分片增加到超过这个点，并以最小的吞吐量成本提高延迟。更多的模型分片为我们提供了更多的 HBM 来加载我们的权重，而我们的 FLOPs 并不重要。意思是 FLOPs 时间不是我们的瓶颈，所以我们需要担心的是 ICI 时间超过参数加载时间。让我们看看在模型并行性成为瓶颈之前，我们可以做多少。

\begin{aligned} T_{HBM comms} = \frac{2 D F}{Y \cdot W_{hbm}} & T_{ICI comms} = \frac{2 B D}{W_{ici}} \end{aligned}

T_{ICI comms} > T_{HBM comms} \to \frac{W_{hbm}}{W_{ici}} > \frac{F}{Y \cdot B} \to Y > F / (B \cdot β)

其中 \beta = W_\text{hbm} / W_\text{ici}。对于 TPU v5e 和 TPU v6e，这个数字通常在 8 左右。这意味着，例如，如果 F 是 16,384，B 是 32，理论上我们可以进行高达 16384 / (32 * 8) = 64 路的模型并行性，而不会对吞吐量产生有意义的影响。这假设我们可以将我们的 KV 缓存完全分片 64 路，这很困难：我们将在下面讨论这个问题。

对于注意力层，我们还以 Megatron 的方式在头上对注意力 $W_{Q}$ 和 $W_{O}$ 进行模型分片。KV 权重相当小，复制它们通常比分片超过 K 路分片更便宜。

要点： 在生成期间，我们唯一的选择是模型并行性的变体。我们的目标是移动激活而不是更大的 KV 缓存或参数。当我们的批量大小很大时，我们进行模型并行性直到达到 FLOPs-ICI 边界（F / \alpha）。当我们的批量大小较小时，我们可以通过更多的模型分片来改善延迟（以适度的吞吐量成本）。当我们想要模型分片的数量超过我们拥有的 KV 头数时，我们也可以沿着批次维度对我们的 KV 进行分片。

分片 KV 缓存

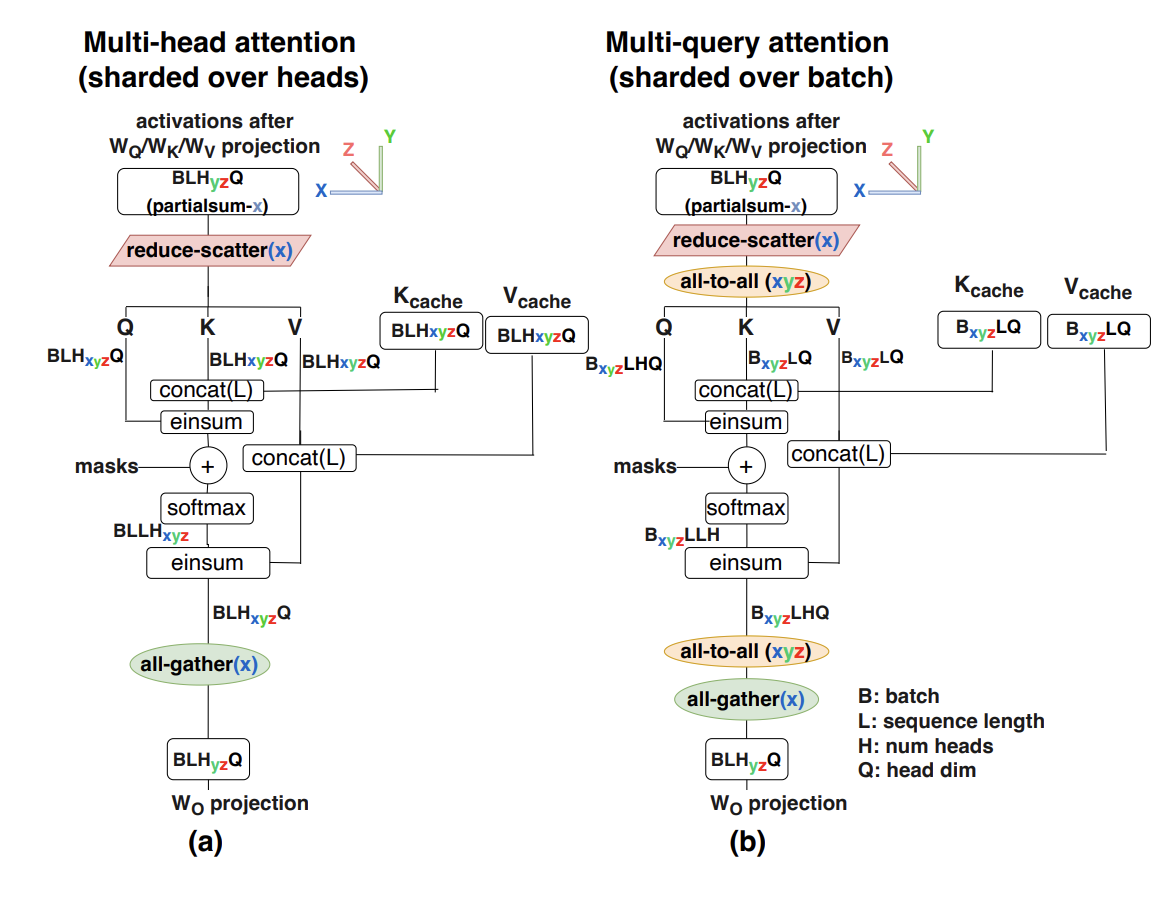
我们还有一个需要分片的额外数据结构——KV 缓存。 同样，我们几乎总是倾向于避免复制缓存，因为它是注意力延迟的主要来源。为此，我们首先沿着头维度对 KV 进行 Megatron 分片。这仅限于 K 路分片，所以对于头数较少的模型，我们尽可能地分片头维度，然后沿着批次维度分片，即 \text{KV}[2, B_Z, S, K_Y, H]。这意味着 KV 缓存是完全分布式的。

图：注意力机制的比较，(a) 具有纯模型分片的多头注意力和 (b) 具有 KV 缓存批次分片的多查询注意力。注意我们如何需要两个额外的 AllToAlls 来将激活从模型分片转移到批次分片，以便它们可以作用于 KV 缓存。

这样做的代价是每个注意力层需要两次 AllToAlls 操作——一次是将 Q 激活转移到批次分片，以便我们可以用批次分片计算注意力；另一次是将批次分片的注意力输出转回纯模型分片。

这是完整的算法！

在这里，我们将写出在 Y 和 Z 上都进行模型并行性的完整注意力算法。我为同时使用 K 表示键张量和 KV 头维度而道歉。设 M=N/K。

X[B, D] = … (现有激活，来自前一层，未分片)
K[B_Z, S, K_Y, H], V[B_Z, S, K, H] = … (现有 KV 缓存，批次分片)
Q[B, N_YZ, H] = X[B, D] * W_Q[D, N_YZ, H]
Q[B_Z, N_Y, H] = AllToAll_Z->B(Q[B, N_YZ, H])
Q[B_Z, K_Y, M, H] = Reshape(Q[B_Z, N_Y, H])
O[B_Z, S, K_Y, M] = Q[B_Z, K_Y, M, H] *_H K[B_Z, S, K_Y, H]
O[B_Z, S, K, M] = Softmax_S(O[B_Z, S, K_Y])
O[B_Z, K_Y, M, H] = O[B_Z, S, K, M] *_S V[B_Z, S, K_Y, H]
O[B, K_Y, M_Z, H] = AllToAll_Z->M(O[B_Z, K_Y, M, H])
O[B, N_YZ, H] = Reshape(O[B, K_Y, M_Z, H])
X[B, D] {U_YZ} = W_O[N_YZ, H, D] *_N,H O[B, N_YZ, H]
X[B, D] = AllReduce(X[B, D] { U_YZ})

这相当复杂，但你可以大致了解它的工作原理。新的通信开销适中，因为它们作用于我们的小激活，作为回报，我们节省了大量的内存带宽来加载 KV（它们是静止的）。

序列分片： 如果批量大小太小，或者上下文很长，我们可以对 KV 缓存进行序列分片。同样，我们在这里为跨分片累积注意力付出了集体通信的代价。首先我们需要 AllGather Q 激活，然后以类似于 Flash Attention 的方式累积 KV。

设计高效的推理引擎

到目前为止，我们已经研究了如何独立地高效优化和分片单个预填充和生成操作。为了实际有效地使用它们，我们需要设计一个推理引擎，它可以在我们选择的延迟/吞吐量帕累托前沿的点上为这两个操作提供数据。

最简单的方法是简单地运行一批预填充，然后运行一批生成：

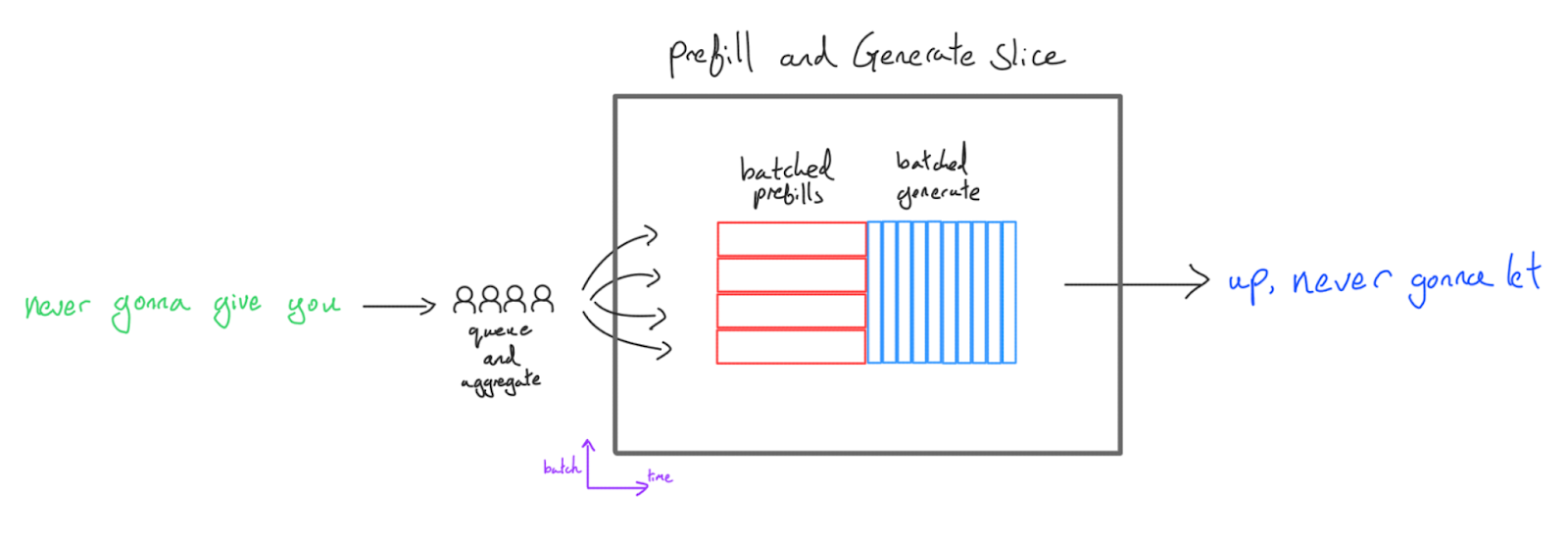
图：在最简单的设置中，请求被聚合，服务器在运行一批预填充和为所有序列调用生成函数直到完成之间交替进行。

这很容易实现，是大多数代码库中的第一个推理设置，但它有多个缺点：

延迟很糟糕。 我们将预填充和生成的批量大小耦合在一起。在大的预填充批量下，首词元时间（TTFT）非常糟糕——你需要完成所有预填充后，用户才能看到任何词元。在小的批量下，生成吞吐量很糟糕。
我们让较短的生成被较长的生成阻塞。 许多序列会比其他序列先完成，在生成期间留下空的批次槽位，进一步损害生成吞吐量。随着批量大小和生成长度的增加，这个问题会加剧。
预填充被填充。 预填充被填充到最长的序列，我们浪费了大量的计算。对此有解决方案，但历史上 XLA 使得跳过这些 FLOPs 相当困难。同样，批量大小和预填充序列长度越大，情况越糟。
我们被迫在预填充和生成之间共享一个分片策略。 预填充和生成都在同一个切片上运行，这意味着我们对两者使用相同的拓扑和分片（除非你保留两份权重副本），这通常对性能无益，例如，生成需要更多的模型分片。

因此，这种方法只推荐用于边缘应用（通常只关心服务单个用户并使用 FLOPs/字节较少的硬件）和 Transformer 代码库生命周期早期的快速迭代（由于其简单性）。

一种稍微好一点的方法是在批量大小为 1 时执行预填充（此时它是计算密集型的，但延迟合理），但在生成期间将多个请求批处理在一起：

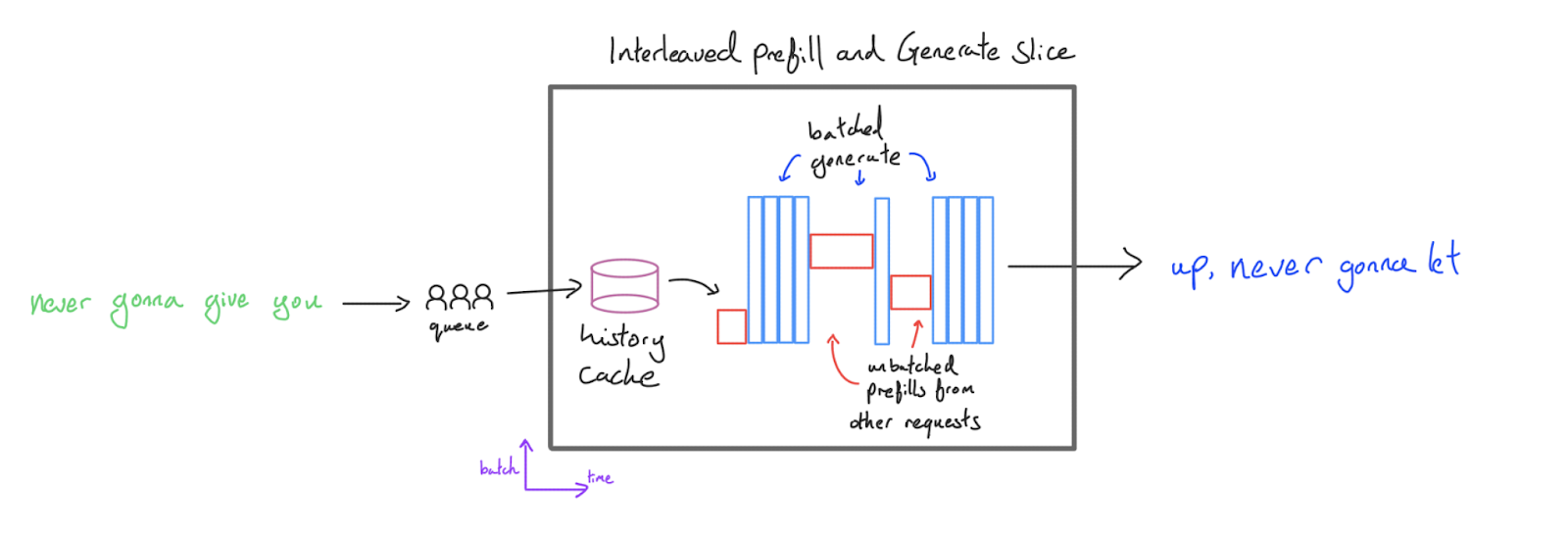
这将避免因批处理预填充而浪费的 TTFT，同时保持较高的生成吞吐量。我们称之为交错配置，因为我们“交错”了预填充和生成步骤。这对于批量生成应用（如评估）非常强大，其中吞吐量是主要目标。协调器可以配置为在任何生成槽位空闲时优先进行预填充，即使对于非常大的生成批量大小也能确保高利用率。我们还可以避免将预填充填充到最大长度，因为它没有与另一个请求批处理。

主要缺点是，当服务器正在执行预填充时，所有其他请求的生成都会暂停，因为所有计算资源都将被预填充消耗。用户 A 的响应正在解码，将被用户 B 的预填充阻塞。这意味着即使 TTFT 得到了改善，词元生成平均也会出现抖动和缓慢，这对许多应用来说不是一个好的用户体验——其他用户的预填充处于请求总延迟的关键路径上。

为了解决这个问题，我们将解码和预填充分开。虽然 Transformer 推理可以在一个服务器上完成，但从延迟的角度来看，将这两个不同的任务在两组 TPU/GPU 上执行通常更好。预填充服务器生成 KV 缓存，这些缓存通过网络发送到生成服务器，生成服务器将多个缓存批处理在一起并为它们中的每一个生成词元。我们称之为“解耦”服务。

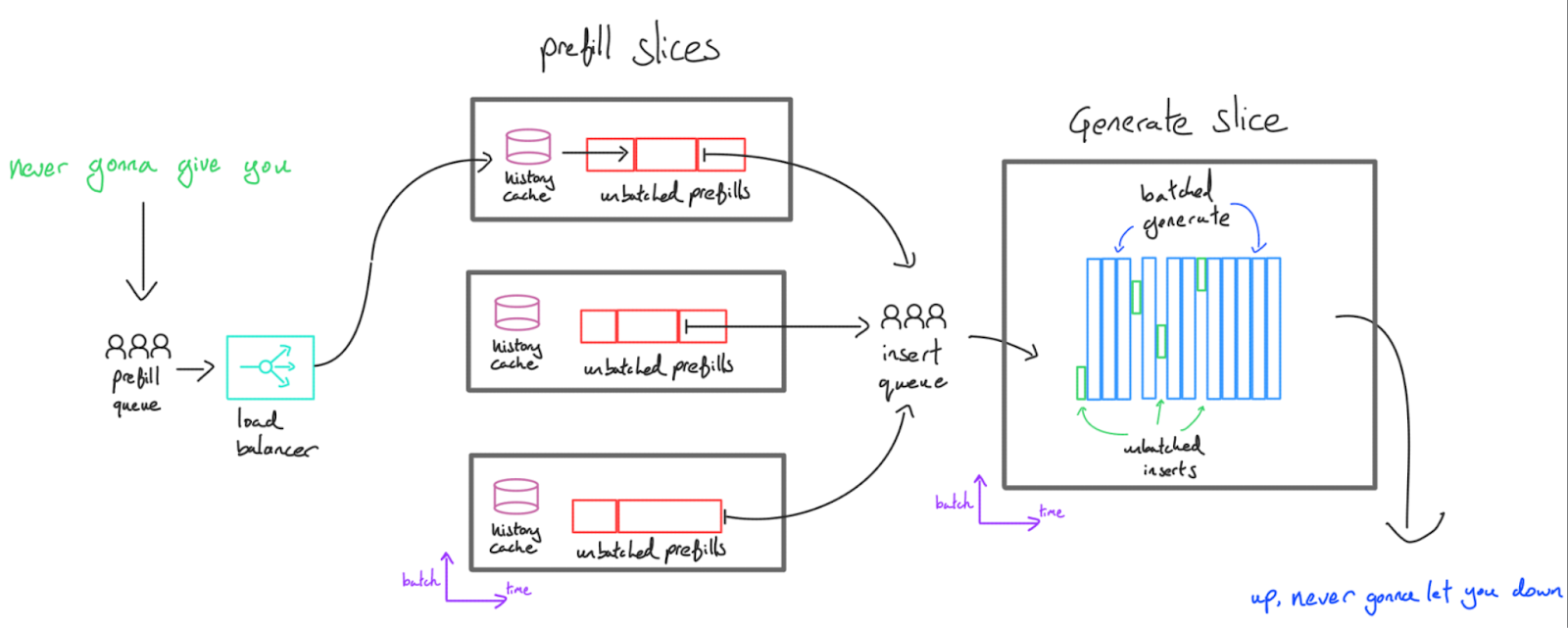
这提供了几个优势：

大规模下的低延迟：用户的请求永远不会被另一个用户的请求阻塞，除非预填充容量不足。请求应该立即被预填充，然后发送到生成服务器，然后立即插入生成缓冲区。如果我们预计会有许多并发请求进来，我们可以独立于生成服务器的数量来扩展预填充服务器的数量，这样用户就不会在预填充队列中等待太长时间。
专业化： 很多时候，预填充和生成的延迟最优参数分片策略/硬件拓扑是相当不同的（例如，更多的模型并行性对生成有用，但对预填充没用）。将这两个操作限制在同一个分片策略下会损害两者的性能，而拥有两套权重会占用内存。此外，通过将预填充移到自己的服务器上，它就不需要持有任何 KV 缓存，除了它当前正在处理的那个。这意味着我们有更多的内存可用于历史缓存（见下一节）或优化预填充延迟。

一个缺点是 KV 缓存现在需要在网络上传输。这通常是可以接受的，但再次为减小 KV 缓存大小提供了动力。

要点： 对于延迟敏感、高吞吐量的服务，我们通常必须将预填充和生成分离到不同的服务器上，预填充以批次 1 运行，而生成则将许多并发请求批处理在一起。

连续批处理

上面的问题 (2) 激发了连续批处理的概念。我们优化并编译：

一些具有可变上下文长度的预填充函数，并将其插入到某个 KV 缓冲区中，该缓冲区具有最大批量大小和上下文长度/页数。
一个生成函数，它接收 KV 缓存，并为所有当前活动的请求执行生成步骤。

然后，我们将这些函数与一个协调器结合起来，该协调器对传入的请求进行排队，根据可用的生成槽位调用预填充和生成，处理历史缓存（见下一节），并以流式方式输出词元。

前缀缓存

由于预填充成本高且受计算限制（给我们留下的空间较少），减少其成本的最佳方法之一就是少做一些。因为 LLM 是自回归的，查询 [“我”, “喜欢”, “狗”] 和 [“我”, “喜欢”, “猫”] 产生的 KV 缓存在前两个词元上是相同的。这意味着，原则上，如果我们先计算“我喜欢狗”的缓存，然后再计算“我喜欢猫”的缓存，我们只需要做 1/3 的计算。我们可以通过重用缓存来节省大部分工作。这在一些特定情况下尤其强大：

聊天机器人：大多数聊天机器人对话都涉及一种严格追加自身的来回对话。这意味着如果我们能保存每次对话轮次的 KV 缓存，我们就可以跳过除最新词元外的所有计算。
少样本提示：如果我们有任何形式的少样本提示，这可以被保存并免费重用。系统指令通常也具有这种形式。

这样做之所以困难，唯一的限制是内存。正如我们所见，KV 缓存很大（通常是几 GB），要使缓存有用，我们需要将它们保留到后续查询到达。通常，预填充服务器上任何未使用的 HBM 都可以用于本地缓存系统。此外，加速器通常在其 CPU 主机上有很多内存（例如，一个 8xTPUv5e 服务器有 128GiB 的 HBM，但大约有 450GiB 的主机 DRAM）。这种内存比 HBM 慢得多——通常慢到无法进行生成步骤——但对于缓存读取来说足够快。在实践中：

因为 KV 缓存是处理初始请求的 TPU 集合的本地缓存，我们需要某种形式的亲和性路由来确保后续查询到达同一个副本。这可能会导致负载均衡问题。
一个更小的 KV 缓存（再次）是有帮助的——它使我们能够在相同数量的空间中保存更多的 KV 缓存，并减少读取时间。
KV 缓存及其查找可以很自然地存储在树或前缀树中。可以基于 LRU（最近最少使用）原则进行驱逐。

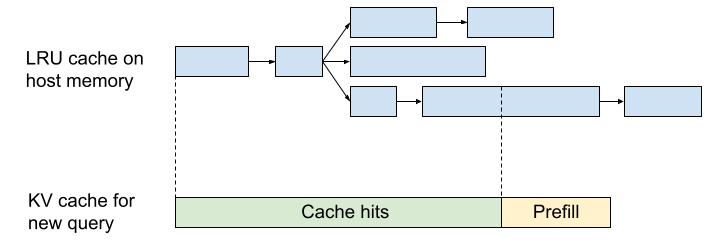
图：以 LRU 前缀树实现的 KV 前缀缓存。我们可以通过共享前缀来避免重复的 KV 内存。来源：Character.ai 博客。

来看一个实现：JetStream

谷歌开源了一个实现这种逻辑的库，名为 JetStream。该服务器有一组“预填充引擎”和“生成引擎”，通常位于不同的 TPU 切片上，由一个控制器进行协调。预填充发生在“预填充线程”中，而生成发生在“生成线程”中。我们还有一个“传输线程”，负责协调将 KV 缓存从预填充切片复制到生成切片。

Engine 接口（在此实现）是任何 LLM 必须提供的通用接口。关键方法是：

prefill: 接收一组输入词元并生成一个 KV 缓存。
insert: 接收一个 KV 缓存并将其插入到生成正在处理的 KV 缓存批次中。
generate: 接收一批 KV 缓存并为每个批次条目生成一个词元，将单个词元的 KV 缓存附加到每个词元的解码状态中。

我们还有一个可用的 PyTorch 版本的 JetStream 在此。

习题

在本节中，我将基于 LLaMA-2 13B 发明一个新模型。以下是详细信息：

超参数	值
L (num_layers)	64
D (d_model)	4,096
F (ffw_dimension)	16,384
N (num_heads)	32
K (num_kv_heads)	8
H (qkv_dim)	256
V (num_embeddings)	32,128

问题 1： 上述模型有多少参数？其 KV 缓存每个词元在 int8 下有多大？你可以假设我们共享输入和输出投影矩阵。

点击此处查看答案。

参数数量：

MLP 参数数量: L * D * F * 3
注意力参数数量: L * 2 * D * H * (N + K)
词汇表参数: D * V (因为我们共享这些矩阵)

因此，我们的总参数数量是 L * D * (3F + 2H * (N + K)) + D * V。代入上面的数字，我们有 64 * 4096 * (3*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 18.4e9。因此，这个模型大约有 184 亿个参数。

KV 缓存是 L * K * H 每个词元，即 64 * 8 * 256 = 131kB 每个词元。

问题 2： 假设我们想在一个 TPUv5e 4x4 切片上服务这个模型，并且可以完全在此拓扑上分片我们的 KV 缓存。假设我们对所有东西都使用 int8，并且希望支持 128k 序列，那么我们能容纳的最大批量大小是多少？如果我们将 KV 头的数量减少到 1 呢？

点击此处查看答案。

我们的 KV 缓存每个词元在 int8 下的大小为 L * K * H，即 64 * 8 * 256 = 131kB。对于 128k 序列，这意味着每个批次条目为 131e3 * 128e3 = 16.8GB。由于每个 TPU 有 16GB 的 HBM，包括我们的参数，我们能容纳的最大批量大小是 (16 * 16e9 - 18.4e9) / 16.8e9 = 14。如果我们有 K=1，我们将拥有这个值的 8 倍，即大约 112。

问题 3： 假设所有参数在 TPU v5e 4x4 切片上完全分片，将它们从 HBM 加载到 MXU 需要多长时间？假设是 int8 参数。这是每步延迟的一个很好的下界。

点击此处查看答案。

我们总共有 18.4B 个参数，在 int8 中是 18.4e9 字节。每个芯片的 HBM 带宽为 8.1e11，所以大约需要 18e9 / (8.1e11 * 16) = 1.3ms，假设我们可以完全利用我们的 HBM 带宽。

问题 4： 假设我们想在一个 TPUv5e 4x4 切片上使用 int8 FLOPs 和参数/激活来服务这个模型。我们将如何为预填充和解码进行分片？提示：也许先回答这些问题：

4x4 上的 ICI 是什么样的？
张量并行性的Roofline界限是什么？
我们如何分片 KV 缓存？

对于这种分片，生成的粗略每步延迟是多少？

问题 5： 让我们假装上述模型实际上是一个 MoE。一个 MoE 模型实际上是一个具有 E 个 FFW 块副本的密集模型。每个词元通过 k 个 FFW 块，并将这 k 个的输出平均以产生最终输出。让我们使用 E=16 和 k=2 以及上述设置。

它有多少总参数和激活参数？激活参数指任何给定词元使用的参数。
在 TPU v5e 上达到 FLOPs 密集型需要多大的批量大小？
它的 KV 缓存每个词元有多大？
一个 T 个词元的正向传播涉及多少 FLOPs？

点击此处查看答案。

(1) 作为一个 MoE，每个 MLP 块现在有 3 * E * D * F 个参数，比密集变体增加了 E 倍。因此，它现在有 L * D * (3EF + 2H * (N + K)) + D * V 或 64 * 4096 * (3*16*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 212e9 个总参数，增加了约 12 倍。对于激活参数，我们有 k 而不是 E 个激活参数，总共为 64 * 4096 * (3*2*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 31.2e9，比密集变体增加了不到 2 倍。

(2) 因为我们的参数增加了 E 倍，而 FLOPs 只增加了 k 倍，我们的 HBM Roofline增加了 E/k 倍。这意味着在 TPU v5e 上，我们需要大约 240 * (16 / 2) = 1920 个词元。

(3) KV 缓存大小保持不变，因为 MoE 的特性不改变任何关于注意力机制的东西。

(4) 这仍然是 2ND，其中 D 是激活参数计数。因此这是 2 * \text{32.2e9} * T。

问题 6： 对于 MoE，我们可以进行“专家分片”，即我们将我们的专家分布在网格的一个轴上。在我们的标准表示法中，我们的第一个 FFW 权重形状为 [E, D, F]，我们将其分片为 [E_Z, D_X, F_Y]，其中 X 仅在训练期间用作我们的 FSDP 维度。假设我们想在 TPU v5e 上进行推理：

在 TPU v5e 8x16 切片上，Y=8, Z=16 时，上述模型的 HBM 权重加载时间是多少？每个 TPU 有多少可用的 HBM？
我们能将我们的模型容纳在的最小切片是多大？

问题 7 [2D 模型分片]： 在这里，我们将详细计算 ESTI 论文中所谓的 2D 权重固定分片。我们在附录 B 中简要描述了这一点，但请先尝试做这个问题，看看你是否能推导出数学。2D 权重固定分片的基本思想是沿着 D 和 F 两个轴对我们的权重进行分片，使得每个块大致是方形的。这减少了通信负载，并允许我们扩展得更远一些。

这是 2D 权重固定的算法：

In[B, D_X] = AllGather_YZ(In[B, D_XYZ])
Tmp[B, F_YZ] {U.X} = In[B, D_X] *_D W_in[D_X, F_YZ]
Tmp[B, F_YZ] = AllReduce_X(Tmp[B, F_YZ] {U.X})
Out[B, D_X] {U.YZ} = Tmp[B, F_YZ] *_F W2[F_YZ, D_X]
Out[B, D_XYZ] = ReduceScatter_YZ(Out[B, D_X] {U.YZ})

你的目标是计算这个算法的 T_\text{math} 和 T_\text{comms}，并找出它何时会优于传统的 3D 模型分片？

点击此处查看答案！

让我们计算 T_\text{math} 和 T_\text{comms}。我们所有的 FLOPs 都是完全分片的，所以和之前一样，我们有 T_\text{math} = 4BDF / (N \cdot C)，但我们的通信现在是

\begin{array}{r} T_{2D comms} = \frac{2 B D}{2 X \cdot W_{ici}} + \frac{4 B F}{Y Z \cdot W_{ici}} + \frac{2 B D}{2 X \cdot W_{ici}} = \frac{2 B D}{X \cdot W_{ici}} + \frac{4 B F}{Y Z \cdot W_{ici}} \end{array}

我们注意到 AllReduce 的成本是原来的两倍，并且我们根据每个操作执行的轴数来缩放我们的通信。假设我们可以自由选择拓扑结构，并假设 F=4D（如 LLaMA-2 中），我们声称（通过一些基本微积分）X、Y 和 Z 的最优值是 X = \sqrt{N / 8}、YZ = \sqrt{8N}，所以总通信量是

T_{2D comms} = \frac{2 B}{W_{ici}} (\frac{D}{X} + \frac{8 D}{Y Z}) = \frac{\sqrt{128} B D}{\sqrt{N} \cdot W_{ici}} \approx \frac{11.3 B D}{\sqrt{N} \cdot W_{ici}}

首先，从上面复制，正常的 1D 模型并行性会有 T_\text{model parallel comms} = 4BD / (3 \cdot W_\text{ici})，那么新的通信何时更小？我们有

\begin{array}{r} T_{model parallel comms} > T_{2D comms} ⟺ \frac{4 B D}{3 \cdot W_{ici}} > \frac{\sqrt{128} B D}{\sqrt{N} \cdot W_{ici}} \\ ⟺ N > 128 \cdot {(\frac{3}{4})}^{2} = 81 \end{array}

对于一个通用的 F，我们声称这个条件是

N > 32 \cdot (\frac{F}{D}) \cdot {(\frac{3}{4})}^{2}

这告诉我们，如果我们有超过 81 个芯片，我们最好使用这个新方案。现在这是一个稍微奇怪的结果，因为我们历史上发现在大约 20 路张量并行性时就受 ICI 限制了。但在这里，即使我们受通信限制，我们的总通信量也会随着总芯片数量的增加而持续减少！这告诉我们，我们可以继续增加我们的芯片，增加我们的批量大小，做更多的参数扩展，并看到延迟降低。

第 7 部分到此结束！关于第 8 部分，我们将探讨如何在 TPU 上服务 LLaMA 3，请点击这里。

附录

附录 A：批量大小 > 240 的规则有多真实？

我们上面提供的简单规则，即我们的批量大小必须大于 240 个词元才能达到计算密集型，这大致是正确的，但忽略了 TPU 在其他操作不使用所有可用 HBM 时（例如进行设备间通信时）预取权重的一些能力。

这是一个小型 Transformer 的层时间（以微秒为单位）的经验图，其中 d_model 为 8192，d_ff 为 32768，每层只有 2 个矩阵乘法。这来自这个 Colab 笔记本。你会看到步长时间在批量大小达到 240 左右之前增长非常缓慢，然后呈线性增长。

这是以词元/微秒为单位的实际吞吐量。这相当清楚地说明了论点。由于我们的层大约有 600M 参数，在这里进行了 4 路分片，我们预计最小延迟大约为 365 微秒。

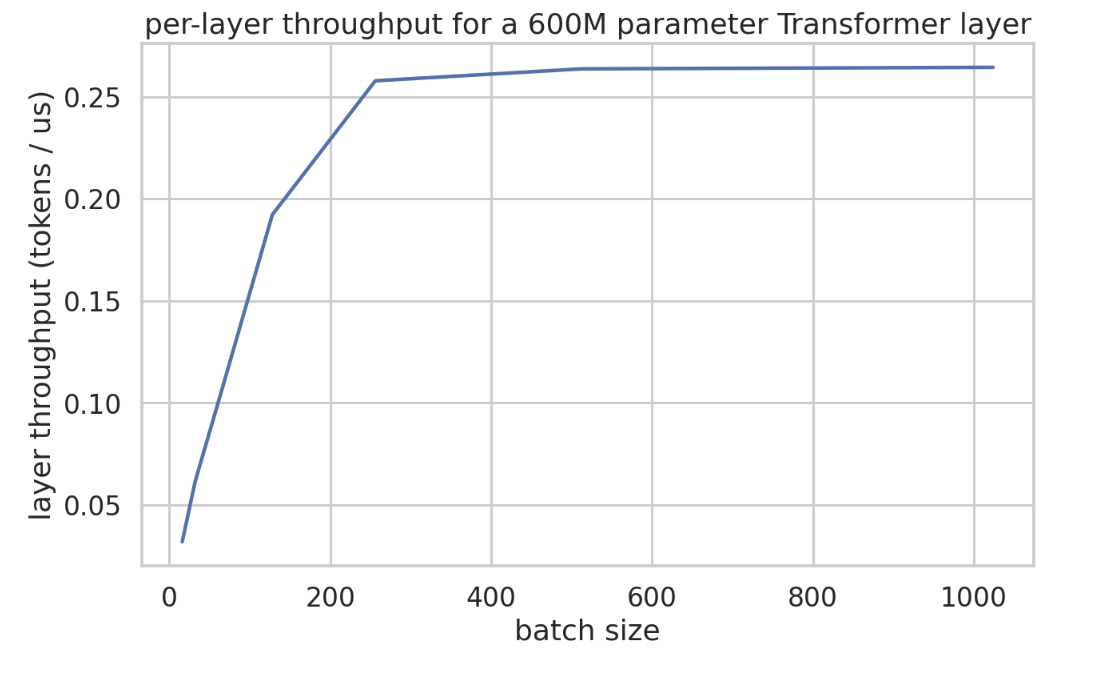
所以至少在这个模型中，我们确实看到吞吐量在每个数据并行分片的 BS 达到约 240 之前一直在增加。

附录 B：2D 权重固定分片

随着拓扑结构的增长，如果我们能接触到更高维度的网格（比如 TPU 的网格），就可以通过“2D 权重分片”进一步优化。通过引入第二个分片轴。我们称之为“2D 权重固定”，在高效扩展 Transformer 推理论文中有更详细的描述。

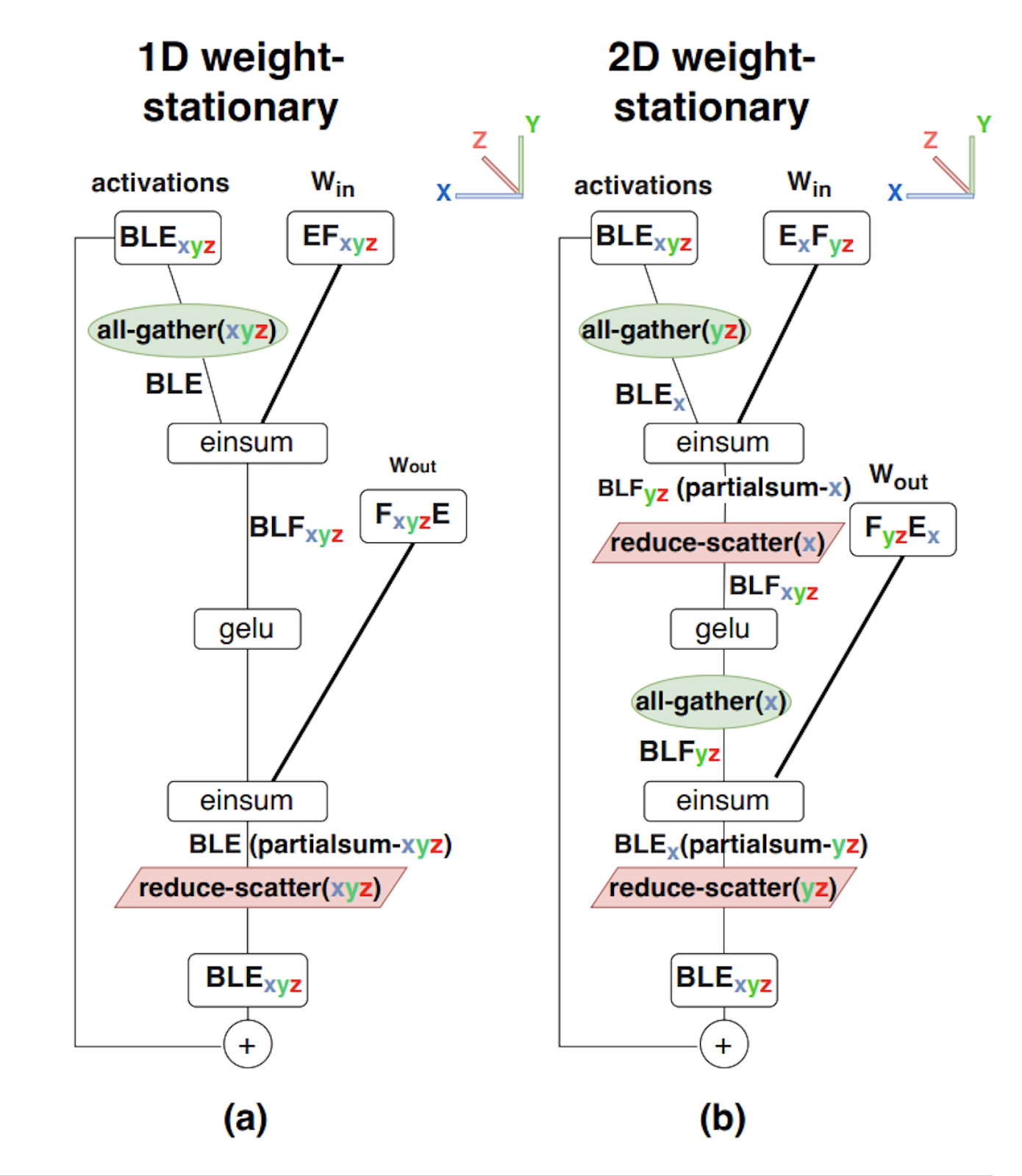
因为在 Megatron 中我们只分片隐藏的 $F$ 维度，一旦芯片数量随着 1D 分片增长，它可能会变得比 $E$ （ $d_{model}$ 维度）小得多。这意味着在较大的批量下，在应用 MLP 的第一层之后，在隐藏维度上执行一部分集合通信可能更经济。

这张图显示：

1D 权重固定分片，即纯 Megatron 分片，其中激活在 AllGather 后完全复制，权重在隐藏的 F 维度上完全分片。
2D 权重固定分片，其中权重在隐藏的 F 维度和缩减的 E 维度上都进行分片，激活在 E 维度上分片。我们在第一层之前在 (yz) 轴上执行 AllGather，然后在 (x) 轴上执行 ReduceScatter。

对于注意力层，对于较少数量的芯片，Megatron 风格的分片也相对简单。然而，Megatron 发生在 $n_{heads}$ 维度上，这对可能的分片量设置了限制。通过修改 2D 分片（不是分片隐藏维度，而是分片 $n_{heads}$ 维度），我们获得了进一步扩展的能力。

附录 C：延迟限制的通信

作为回顾，在第 3 节中，我们推导了在每个 TPU 上，通过 X 个芯片在全双工带宽为 WICI 和延迟为 Tmin 的 1D 环形链路上，对大小为 B 的张量执行 AllGather 所需的时间。

T_{t o t a l} = max (\frac{T_{m i n} \cdot | X |}{2}, \frac{B}{W_{I C I}})

对于大的 B，挂钟时间保持相对恒定，因为当你向系统中添加更多芯片时，你同时扩展了执行操作所需的数据移动量和可用的总带宽。

由于在延迟优化的推理过程中移动的数据量相对较少，对激活的集合操作通常受延迟项的限制（特别是对于小批量大小）。通过计算完成操作所需的跳数，可以很容易地将延迟可视化。

在 TPU 上，如果通信中依赖于张量大小的部分每跳小于 1 微秒（一跳是两个相邻设备之间的通信），我们可能会被实际分派集合操作的固定开销所瓶颈。在 4.5e10 单向 ICI 带宽下，当 $(bytes / n_{shards}) / 4.5 e 10 < 1 e - 6$ 时，ICI 通信会受延迟限制。对于 8 路 Megatron 分片，这是当 buffer_size < 360kB 时。这在推理过程中实际上并不小： 当 BS=16 且 D=8192 在 int8 中，我们的激活将使用 16*8192=131kB，所以我们已经受延迟限制了。

要点： 当 $total bytes < W_{I C I} \times 1 e - 6$ 时，我们的通信会受延迟限制。例如，在 $Y$ 上进行模型并行性时，当 $Y > B D / 45, 000$ 时，我们在 int8 中会受限。

这里可以与计算Roofline做一个类比——我们正在为一些小操作承担固定成本（通信的延迟，矩阵乘法的内存带宽）。

附录 D：推测采样

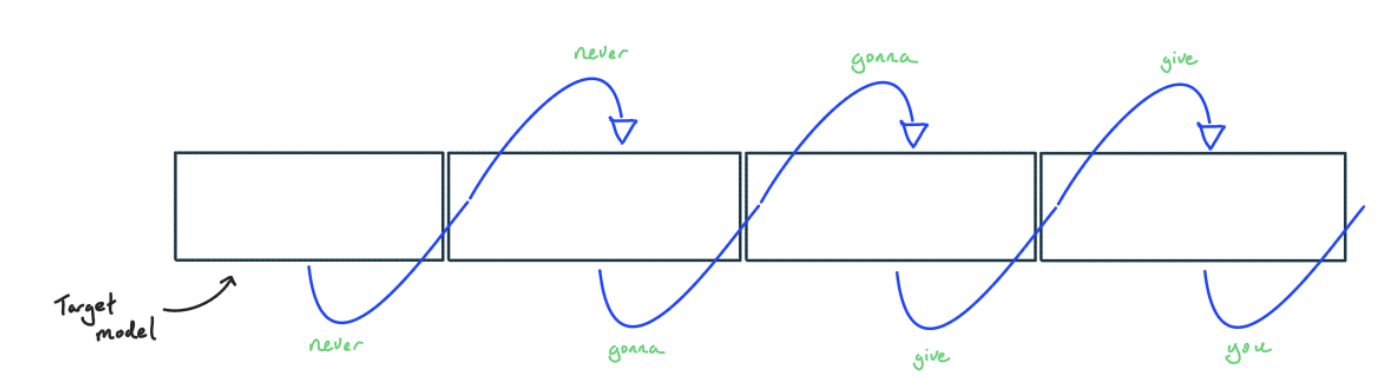
当我们真正关心端到端延迟时，还有一个额外的技巧我们可以使用，叫做推测采样。回顾一下，我们通常从一个大的 Transformer 中逐个生成词元：

通过推测采样，我们使用一个更小、更便宜的模型来生成词元，然后用大模型检查结果。这在贪婪解码中最容易理解：

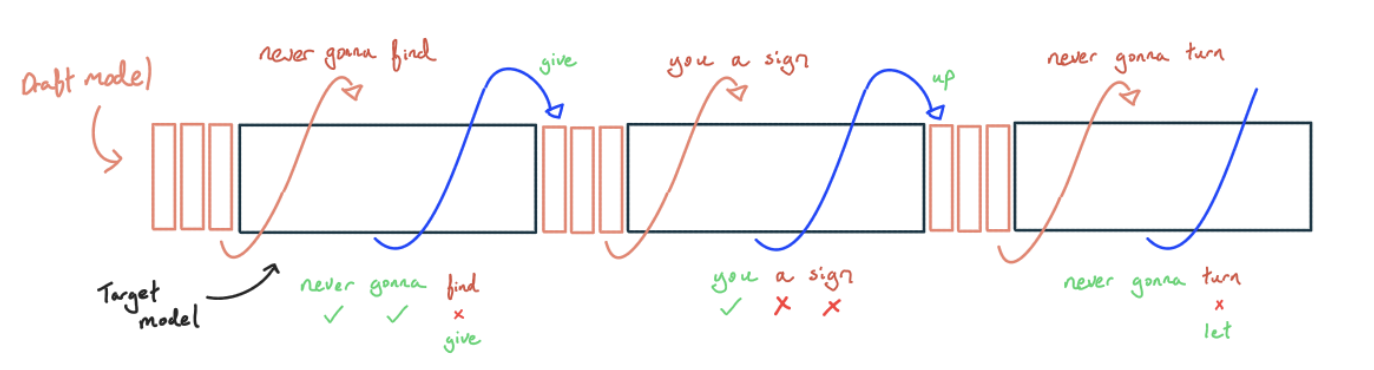
我们从某个更小、更便宜的模型中进行贪婪采样。理想情况下，我们使用一个经过训练以匹配较大模型的模型，例如通过蒸馏，但它也可以像使用 n-gram 或匹配一小部分文本语料库的词元一样简单。
在我们生成了 K 个词元后，我们使用大模型计算我们到目前为止生成的所有词元的下一个词元 logits。
由于我们是贪婪解码，我们可以简单地检查由较小模型生成的词元是否是所有可能词元中概率最高的。如果其中一个词元是错误的，我们取最长的正确前缀，并将第一个错误的词元替换为正确的词元，然后回到（1）。如果所有词元都是正确的，我们可以使用最后一个正确的 logit 来采样一个额外的词元，然后再回到（1）。

为什么这能赢得延迟？ 这个方案仍然要求我们为每个词元做相当于大模型一次前向传播的 FLOPs，但因为我们可以将一堆词元批处理在一起，我们可以在一次前向传播中完成所有这些 FLOPs，并利用我们不是计算密集型的优势来免费评分更多词元。

平均而言，每个被接受的词元在 FLOPs 方面变得更昂贵（因为有些会被拒绝，而且我们必须调用一个草稿模型），但我们从硬件中榨取了更多的 FLOPs，而且小模型很便宜，所以我们总体上赢了。我们还在多个步骤中共享 KV 缓存加载，所以对于长上下文，推测解码也可以在吞吐量上获胜。 由于所有内容都经过了大模型的检查，我们完全没有改变采样分布（尽管对于非贪婪解码，确切的轨迹会有所不同）。

传统上，推测解码依赖于存在一个与目标模型具有相似采样分布的较小模型，例如 LLaMA-2 2B 用于 LLaMA-2 70B，但这通常不存在。即使有，如果接受率低，较小的草稿模型仍然可能太昂贵。相反，将草稿模型嵌入到主模型中可能会有所帮助，例如通过在基础模型的较后层添加一个专用的草稿头。因为这个头与主模型共享大部分参数，所以运行起来更快，并且更紧密地匹配采样分布。

对于正常的自回归采样，词元/秒与步长时间相同。我们仍然受制于这里算术强度部分的理论最小步长时间（实际上，推测采样的步长时间通常比正常自回归采样慢得多，但因为我们平均每步得到超过 1 个词元，所以我们可以得到更好的词元/秒）。

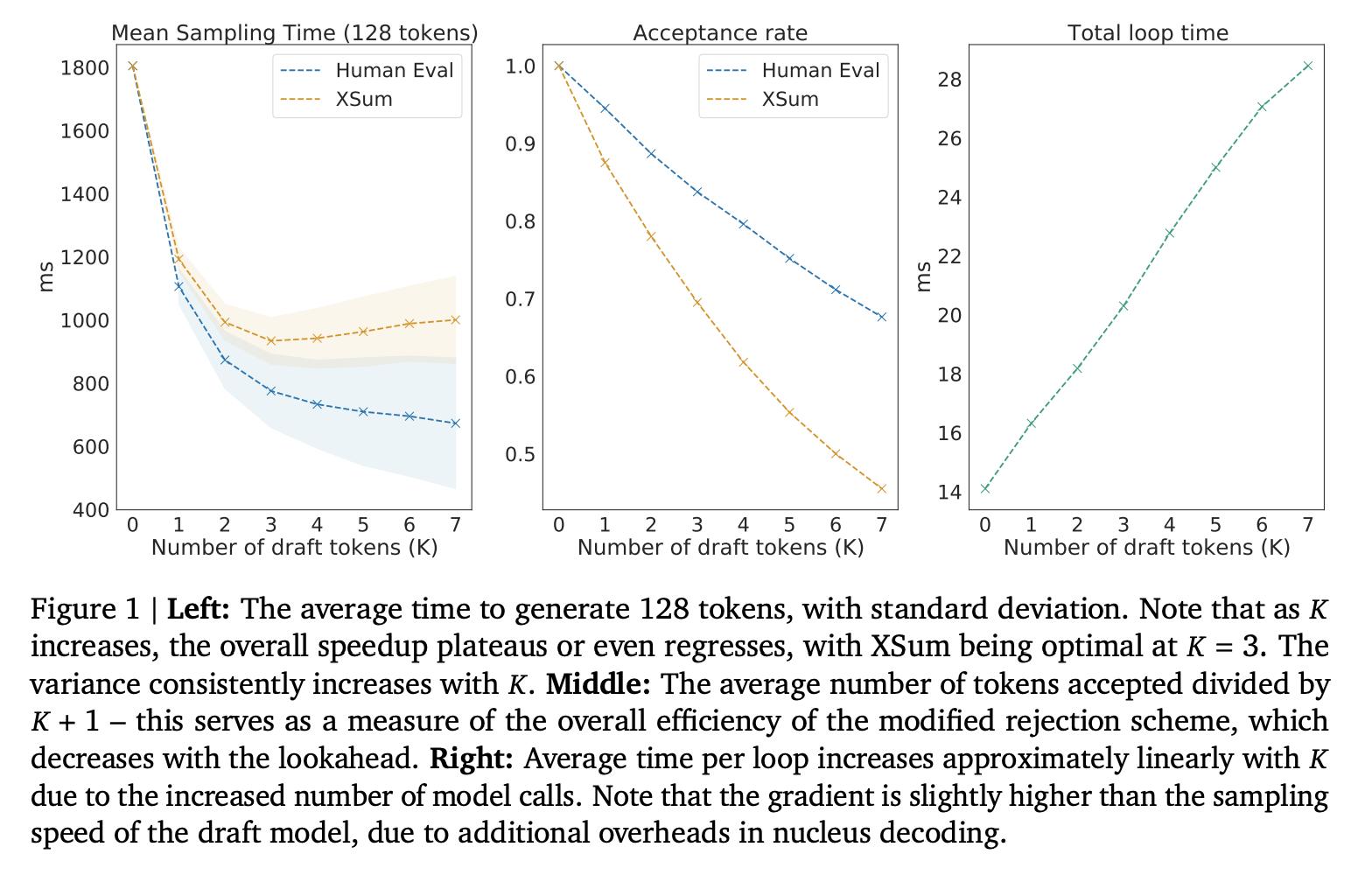
图：这张图显示了 Chinchilla（一个来自 DeepMind 的 70B 模型）和一个 4B 参数的草稿模型（小模型）的每步延迟和推测成功率。对于 XSum（一个自然语言数据集），理想的推测量大约是提前 3-4 个词元，而 HumanEval（一个编码数据集）更可预测，从更激进的推测中获益。

这对于非贪婪解码是如何工作的？ 这有点复杂，但基本上可以归结为一个受 Metropolis-Hastings 启发的算法，其中我们有从 logits 派生出的 $P_{draft model} (chosen token)$ 和 $P_{target model} (chosen token)$ ，如果这些概率的比率小于某个阈值，则以概率方式拒绝所选的词元。

这两篇论文同时推导出了这一点，并提供了很好的实际应用示例。

要点： 推测采样是另一个强大的杠杆，用于以吞吐量换取更好的每词元延迟。然而，在批量大小受限的情况下（例如，硬件占用空间小或 KV 缓存大），它变成了双赢。

脚注

从历史上看，你可以在完全不接触推理的情况下，对 Transformer 进行大量研究——LLM 损失、多项选择基准测试都可以在没有合适的 KV 缓存或生成循环实现的情况下高效运行。这意味着，尤其是在研究代码库中，推理代码路径上通常有很多容易摘取的低垂果实。[↩]
在本节中，你会注意到一件事，那就是推理远不如训练那样宽容。我们通常拥有的 FLOPs 要少得多，批处理的机会也更少，而且对延迟的敏感度要高得多。KV 缓存也极大地复杂化了推理。[↩]
我们在这里做了相当多的简化，忽略了应用 softmax、掩码等操作中的非矩阵乘法 FLOPs。它们应该与计算或 HBM 读取重叠，但在某些 TPU 代上实现起来可能不简单。这些细节不会改变主要信息，即 KV 缓存通常是受内存限制的。[↩]
特别要感谢 Flash Attention，它避免了将我们的注意力矩阵实例化[↩]
训练后不小心保留它是导致数量级性能下降的一个简单而常见的方式[↩]
我们的意思是，以较小的批量大小启动多个带有模型副本的服务器。模型级别的数据并行性严格来说更差。[↩]
意思是 FLOPs 时间不是我们的瓶颈，所以我们需要担心的是 ICI 时间超过参数加载时间。[↩]

参考文献

Efficiently scaling Transformer inference
Pope, R., Douglas, S., Chowdhery, A., Devlin, J., Bradbury, J., Levskaya, A., Heek, J., Xiao, K., Agrawal, S. and Dean, J., 2022. arXiv [cs.LG].
Efficient memory management for large language model serving with PagedAttention
Kwon, W., Li, Z., Zhuang, S., Sheng, Y., Zheng, L., Yu, C.H., Gonzalez, J.E., Zhang, H. and Stoica, I., 2023. arXiv [cs.LG].
Fast inference from Transformers via speculative decoding
Leviathan, Y., Kalman, M. and Matias, Y., 2022. arXiv [cs.LG].
Accelerating large language model decoding with speculative sampling
Chen, C., Borgeaud, S., Irving, G., Lespiau, J., Sifre, L. and Jumper, J., 2023. arXiv [cs.CL].
EAGLE: Speculative Sampling Requires Rethinking Feature Uncertainty
Li, Y., Wei, F., Zhang, C. and Zhang, H., 2024. arXiv [cs.LG].
Medusa: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads
Cai, T., Li, Y., Geng, Z., Peng, H., Lee, J., Chen, D. and Dao, T., 2024. arXiv [cs.LG].
DeepSeek-V3 Technical Report
{DeepSeek-AI},, Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Guo, D., Yang, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Zhang, H., Ding, H., Xin, H., Gao, H., Li, H., Qu, H., Cai, J.L., Liang, J., Guo, J., Ni, J., Li, J., Wang, J., Chen, J., Chen, J., Yuan, J., Qiu, J., Li, J., Song, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Xu, L., Xia, L., Zhao, L., Wang, L., Zhang, L., Li, M., Wang, M., Zhang, M., Zhang, M., Tang, M., Li, M., Tian, N., Huang, P., Wang, P., Zhang, P., Wang, Q., Zhu, Q., Chen, Q., Du, Q., Chen, R.J., Jin, R.L., Ge, R., Zhang, R., Pan, R., Wang, R., Xu, R., Zhang, R., Chen, R., Li, S.S., Lu, S., Zhou, S., Chen, S., Wu, S., Ye, S., Ye, S., Ma, S., Wang, S., Zhou, S., Yu, S., Zhou, S., Pan, S., Wang, T., Yun, T., Pei, T., Sun, T., Xiao, W.L., Zeng, W., Zhao, W., An, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Li, X.Q., Jin, X., Wang, X., Bi, X., Liu, X., Wang, X., Shen, X., Chen, X., Zhang, X., Chen, X., Nie, X., Sun, X., Wang, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yu, X., Song, X., Shan, X., Zhou, X., Yang, X., Li, X., Su, X., Lin, X., Li, Y.K., Wang, Y.Q., Wei, Y.X., Zhu, Y.X., Zhang, Y., Xu, Y., Xu, Y., Huang, Y., Li, Y., Zhao, Y., Sun, Y., Li, Y., Wang, Y., Yu, Y., Zheng, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Tang, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Wu, Y., Ou, Y., Zhu, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Zha, Y., Xiong, Y., Ma, Y., Yan, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Wu, Z.F., Ren, Z.Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Huang, Z., Zhang, Z., Xie, Z., Zhang, Z., Hao, Z., Gou, Z., Ma, Z., Yan, Z., Shao, Z., Xu, Z., Wu, Z., Zhang, Z., Li, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Gao, Z. and Pan, Z., 2024. arXiv [cs.CL].

杂项

^*在 Google DeepMind 完成的工作，现就职于 MatX。

引用

在学术背景下进行引用，请将此作品引用为：

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

或作为 BibTeX 条目：

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }