🔗 英文原文： https://jax-ml.github.io/scaling-book/transformers/
✍️ 翻译： 北极的树
微信二维码 微信公众号

你需要知道的所有Transformer数学知识

《如何扩展你的模型》第4部分 (第3部分：分片 | 第5部分：训练)

在这里，我们将快速回顾Transformer架构，特别是如何计算FLOPs、字节数和其他感兴趣的量。

作者

单位

Jacob Austin

Google DeepMind

Sholto Douglas

Roy Frostig

Anselm Levskaya

Charlie Chen

Sharad Vikram

Federico Lebron

Peter Choy

Vinay Ramasesh

Albert Webson

Reiner Pope*

发布日期

2025年2月4日

点积计算

让我们从向量\(x\)、\(y\)和矩阵\(A\)、\(B\)开始，它们的形状如下：

\[\def \red#1{\textcolor{red}{#1}} \def \green#1{\textcolor{green}{#1}} \def \blue#1{\textcolor{blue}{#1}} \def \purple#1{\textcolor{purple}{#1}} \def \orange#1{\textcolor{orange}{#1}} \def \gray#1{\textcolor{gray}{#1}} \begin{array}{cc} \textrm{数组} & \textrm{形状} \\ \hline x & \textrm{[P]} \\ y & \textrm{[P]} \\ A & \textrm{[N P]} \\ B & \textrm{[P M]} \\ \hline \end {array}\] \[\begin{array}{ccc} \textrm{操作} & \textrm{FLOPs} & \textrm{数据} \\ \hline x \cdot y & 2P & 2P \\ A x & 2NP & NP + P \\ AB & 2NPM & NP + PM \\ [c_0,...,c_N] \cdot [d_0,...,d_N] & 2 \prod c_i \times \prod_{\substack{d_j \notin \blue{BATCH} \\ d_j \notin \red{CONTRACT}}} d_j & \prod c_i + \prod d_j \\ \hline \end {array}\]

请注意，对于矩阵-矩阵乘法，计算量以立方级（\(O(N^3)\)）增长，而数据传输仅以平方级（\(O(N^2)\)）增长——这意味着随着我们扩大矩阵乘法的规模，达到计算饱和的极限变得更容易。这是极不寻常的，并且在很大程度上解释了为什么我们使用以矩阵乘法为主的架构——它们易于扩展！

前向和反向FLOPs

在训练期间，我们并不特别关心给定矩阵乘法的结果；我们真正关心的是它的导数。这意味着我们在反向传播期间会进行更多的FLOPs。

如果我们假设B只是一个更大网络中的一个矩阵，而A是我们的输入激活，其中C = A B，则损失L相对于B的导数由链式法则给出：

\[\frac{\partial L}{\partial B} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial B} = A^T \left(\frac{\partial L}{\partial C}\right)\]

这是一个外积，需要2NPM FLOPs来计算（因为它在\(N\)维度上收缩）。同样，损失相对于A的导数为

\[\frac{\partial L}{\partial A} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial A} = \left(\frac{\partial L}{\partial C}\right) B^T\]

同样是2NPM FLOPs，因为dL/dC是一个大小为\[N, M\]的（余）向量。虽然这个量不是相对于参数的导数，但它被用来计算网络前几层的导数（例如，就像dL/dC被用来计算上面的dL/dB一样）。

将这些加起来，我们看到在训练期间，我们总共有6NPM FLOPs，而在推理期间是2NPM：前向传播2NPM，反向传播4NPM。由于PM是矩阵中的参数数量，这是著名的\(6 * \text{参数数量} * \text{token数量}\)近似Transformer训练期间FLOPs的最简单形式：每个token需要\(6 * \text{参数数量}\) FLOPs。我们将在下面展示一个更正确的推导。

Transformer计算分析

Transformer是未来。嗯，至少它们是现在。也许几年前，它们是众多架构之一。但今天，几乎值得了解该架构的每一个细节。我们不会重新介绍该架构，但这篇博客和原始Transformer论文可能会是很有帮助的参考资料。

以下是Transformer解码器架构的基本示意图：

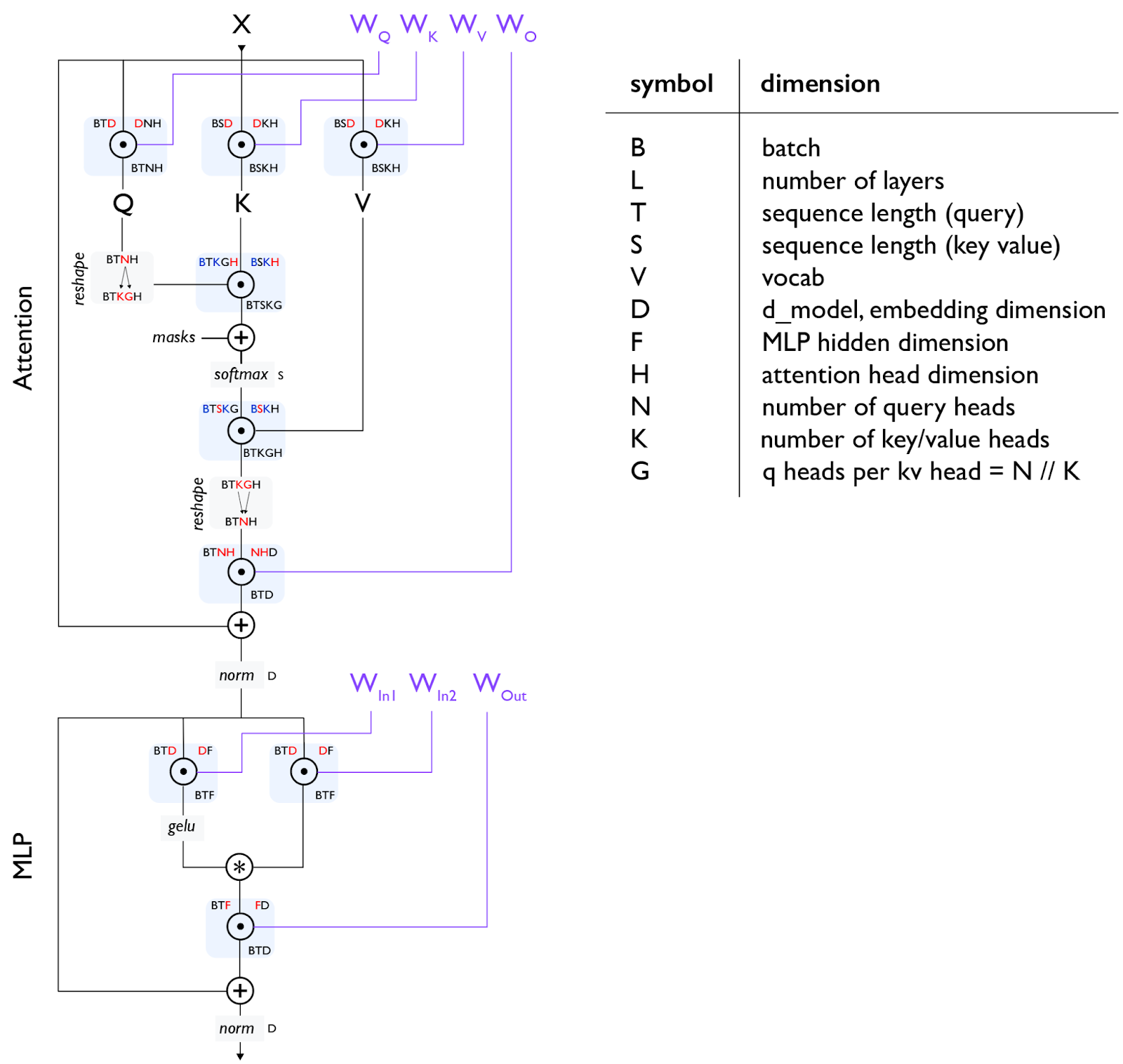
图：该图展示了一个标准Transformer的一层，数据流从上到下。我们使用单字母约定来描述Transformer中数组的形状和布局，再次用红色表示收缩维度，用蓝色表示批处理维度。在给定的操作中，左上角是输入形状，右上角是参数形状，下方是结果形状，例如，BTD是门控einsum的输入形状，DF是权重形状。

注意 [门控einsum]：上图使用了一种“门控einsum”，其中我们将上投影矩阵分成两个矩阵（上图中的\(W_\text{In1}\)和\(W_\text{In2}\)），其输出被逐元素相乘以作为一种“门控函数”。并非所有LLM都使用这种方法，所以你有时会看到一个单独的\(W_\text{In}\)矩阵，总MLP参数数量为2DF而不是3DF。通常在这种情况下，D和F会被放大以保持参数数量与3矩阵情况相同。话虽如此，LLAMA、DeepSeek和许多其他模型都使用了某种形式的门控einsum。

注意2 [MHA注意力]：对于自注意力，T和S是相同的，但对于交叉注意力，它们可能不同。对于普通的多头注意力（MHA），N和K是相同的，而对于多查询注意力（MQA），K=1，对于分组MQA（GMQA），K只需能整除N即可。

全局FLOPs和参数计算

为了避免到处都写上L因子，下面我们将计算每层的FLOPs。

MLP

Transformer的MLP通常由2个输入矩阵乘法（其结果逐元素组合）和1个输出矩阵乘法组成：

\[\begin{array}{ccc} \textrm{操作} & \textrm{训练 FLOPs} & \textrm{参数} \\ \hline \\ A[B,T,\red{D}] \cdot W_{in1}[\red{D}, F] & 6BTDF & DF \\[10pt] A[B,T,\red{D}] \cdot W_{in2}[\red{D}, F] & 6BTDF & DF \\[10pt] \sigma\left(A_{in1}\right)[B,T, F] * A_{in2}[B,T, F] & \gray{O(BTF)} \\[10pt] A[B,T,\red{F}] \cdot W_{out}[\red{F}, D] & 6BTDF & DF \\[10pt] \hline \\ & \approx 18BTDF & 3DF \end{array}\]

注意力

对于具有不同Q和KV头数的通用分组查询注意力情况，我们假设Q、K、V投影的头维度H相等，并估计QKVO矩阵乘法的成本：

\[\begin{array}{ccc} \textrm{操作} & \textrm{训练 FLOPs} & \textrm{参数} \\ \hline \\ A[B,T,\red{D}] \cdot W_{Q}[\red{D}, N, H] & 6BTDNH & DNH \\[10pt] A[B,T,\red{D}] \cdot W_{K}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{D}] \cdot W_{V}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{N}, \red{H}] \cdot W_{O}[\red{N}, \red{H}, D] & 6BTDNH & DNH \\[10pt] \hline \\ & 12BTD(N+K)H & 2D(N+K)H \end{array}\]

点积注意力操作更为精细，实际上是在\(B\)、\(K\)维度上批处理的\(TH \cdot HS\)矩阵乘法，一个softmax，以及再次在\(B\)、\(K\)维度上批处理的\(TS \cdot SH\)矩阵乘法。我们用蓝色突出显示批处理维度：

\[\begin{array}{cc} \textrm{操作} & \textrm{训练 FLOPs} \\ \hline \\[3pt] Q[\blue{B}, T, \blue{K}, G, \red{H}] \cdot K[\blue{B}, S, \blue{K}, \red{H}] & 6BTSKGH = 6BTSNH \\[3pt] \textrm{softmax}_S \;\; L[B, T, S, K, G] & \gray{O(BTSKG) = O(BTSN)} \\[3pt] S[\blue{B}, T, \red{S}, \blue{K}, G] \cdot V[\blue{B}, \red{S}, \blue{K}, H] & 6BTSKGH = 6BTSNH \\[3pt] \hline \\ & \approx 12BTSNH = 12BT^2NH \\ \end{array}\]

其他操作

在Transformer中还有其他几种操作。层归一化（Layernorm）相对便宜，在一阶成本估算中可以忽略。还有一个最终的巨大（但不是每层都有）的unembedding矩阵乘法。

\[\begin{array}{ccc} \textsf{操作} & \textsf{训练 FLOPs} & \textsf{参数} \\ \hline \\ \textrm{layernorm}_D \;\; A[B,T,\red{D}] & \gray{O\left(BTD\right)} & \gray{D} \\[10pt] A[B,T,\red{D}] \cdot W_{unembed}[\red{D}, V] & 6BTDV & DV \\ \end{array}\]

Transformer FLOPs的通用经验法则

如果我们忽略短上下文训练中点积注意力的成本，那么所有层的总FLOPs为

\[\begin{align*} (18BTDF + 12BTD(N+K)H)L = 6 *BT * (3DF + 2D(N+K)H)L \\ = 6 * \textrm{token数量} * \textrm{参数数量} \end{align*}\]

这就得出了一个著名的经验法则，用于估算密集Transformer的FLOPs数量，忽略了注意力的FLOPs。（Unembedding是另一个简单的矩阵乘法，有6BSDV FLOPs和DV参数，遵循相同的经验法则。）

注意力成本在上下文长度中的占比

如果我们确实考虑了上面的点积注意力，并假设\(F=4D\)，\(D=NH\)（通常如此）和\(N=K\)：

\[\small{\frac{\textrm{注意力 FLOPs}}{\textrm{矩阵乘法 FLOPs}} = \frac{12BT^2NH}{18BTDF + 24BTDNH} = \frac{12BT^2D}{4*18 BTD^2 + 24 BTD^2} = \frac{12BT^2D}{96 BTD^2} = \frac{T}{8D}}\]

因此，结论是点积注意力的FLOPs仅在训练期间T>8D时才占主导地位。对于D约等于8k，这将是约64K个token。这在某种程度上是合理的，因为它意味着随着MLP大小的增加，注意力的FLOPs变得不那么关键。对于大型模型，注意力的二次成本实际上并不是长上下文训练的巨大障碍。然而，对于较小的模型，例如Gemma-27B，D=4608，这意味着注意力在序列长度约32k时开始占主导地位。Flash Attention也有助于减轻长上下文的成本，我们将在附录A中简要讨论。

其他数学知识

稀疏性与专家混合模型

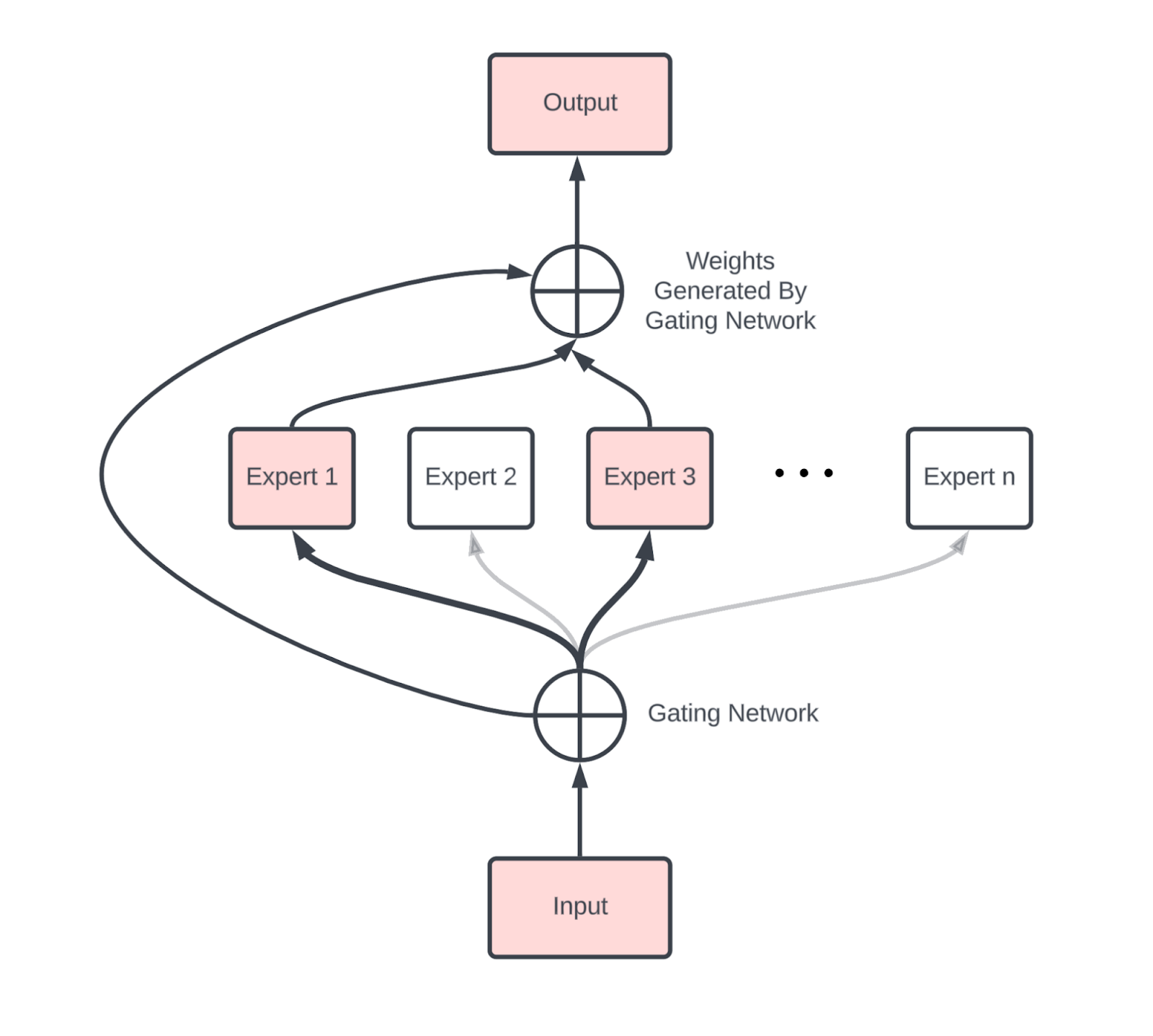
我们不能不简要讨论一下专家混合（MoE）模型，它用一组可以动态路由的独立MLP替换了标准Transformer中的单个密集MLP块。初步近似，一个MoE模型就是一个每层有E个MLP块的普通密集模型，而不是只有一个。每个token激活其中\(k\)个专家，通常\(k=2\)。与密集版本相比，这将参数数量增加了\(O(E)\)倍，同时将每个token激活的总参数数量乘以\(k\)倍。

图：一个有\(n\)个专家的MoE层示例。门控专家将每个token路由到其中的\(k\)个，这\(k\)个MLP的输出被求和。我们的参数数量是每个专家大小的\(n\)倍，但每个token只使用\(k\)个。来源。

与密集模型相比，MoE引入了新的通信，主要是两个AllToAll操作（一个在MoE块之前，一个在之后），用于将token路由到正确的专家，并将它们带回其宿主设备。严格来说，这只在我们沿专家所在的同一轴进行数据或序列分片时才会发生。然而，正如我们在上一节中看到的，每个AllToAll的成本仅为沿单个轴（对于双向环）的可比AllGather成本的1/4。

梯度检查点

反向传播作为一种算法，是用内存换取计算。反向传播不再需要\(O(n_\text{layers}^2)\)的FLOPs，而是需要\(O(n_\text{layers})\)的内存，保存前向传播期间生成的所有中间激活。虽然这比二次计算要好，但在内存方面却非常昂贵：一个拥有\(B * T=4M\)（每批次总共4M个token）、L=64和D=8192的模型，如果避免所有不必要的反向传播计算，将不得不以bfloat16格式保存大约\(2 * 20 * B * T * D * L = 84TB\)的激活。这里的20（大致）来自于计算上图Transformer图中的每个中间节点，因为例如

\[f(x) = \exp(g(x))\] \[\frac{df}{dx} = \exp(g(x)) \cdot \frac{dg}{dx}\]

因此为了避免重新计算，我们需要保存前向传播中的\(g(x)\)和\(\exp(g(x))\)。为了避免保存这么多内存，我们可以选择只保存一部分中间激活。以下是我们使用的几种策略。

这绝不是全面的。在使用JAX时，这些通常由jax.remat/jax.checkpoint控制（你可以在这里阅读更多）。

键值（KV）缓存

正如我们将在第7节中看到的，LLM推理有两个关键部分，预填充（prefill）和生成（generation）。

每个KV缓存实际上是一个大小为[2, S, L, K, H]的数组，其中2代表键和值。这相当大！以int8格式存储的键值缓存总大小为2SLKH。对于一个中等规模的模型，上下文长度为8k，有64层，且KH = NH = D = 8192，这将是2 \cdot 8192 \cdot 64 \cdot 8192 = 8\text{GiB}。你可以看到为什么我们想要使用GMQA，其中K \ll N。

本节要点总结

组件 每层参数 每层训练FLOPs
MLP 3DF 18BTDF
注意力 4DNH 24BTDNH + 12BT2NH
其他 D BTD
词汇表 DV（总计，非每层） 12BTDV

几个练习题

问题1： 一个模型，其D=4096，F=4 \cdot D，V=32,000，L=64，有多少参数？其中注意力参数占多大比例？每个token的KV缓存有多大？你可以假设N\cdot H=D和多头注意力，使用int8 KVs。

点击这里查看答案。
  1. 总参数大约是 \(L \cdot (3DF + 4DNH + D) + 2DV\)。对于给定的数字，这是 \(64 \cdot (3 \cdot 4e3 \cdot 16e3 + 4 \cdot 4e3 \cdot 4e3 + 4e3) + 2 \cdot 4e3 \cdot 32e3 = 16e9\)，即16B参数。
  2. 注意力参数与总参数的比例通常是 \(4DNH / (4DNH + 3DF) = 4D^2 / (4D^2 + 12D^2) = 1/4\)。这告诉我们大约1/4的参数用于注意力。
  3. 每个token，我们的KV缓存是 \(2 \cdot L \cdot N \cdot H = 2 \cdot 64 \cdot 4096\)（int8格式），即512kB / token。

问题2： 在{'X': 4, 'Y': 8, 'Z': 4}上执行 A[BX, DY] *D W[DY, F] 需要多少总FLOPs？每个TPU执行多少FLOPs？

点击这里查看答案。

该操作的总“理论”FLOPs是 \(2 \cdot B \cdot D \cdot F\)。然而，因为计算没有在Z维度上分片，我们实际上多做了Z倍的FLOPs，意味着总FLOPs为 \(2 \cdot B \cdot D \cdot F \cdot Z\)。由于计算在其他维度上是分片的，每个设备的总FLOPs大约是 \(2 \cdot B \cdot D \cdot F / (X \cdot Y)\)。

问题3： 执行A[I,J,K,L] * B[I,J,M,N,O] \rightarrow C[K,L,M,N,O]涉及多少FLOPs？

点击这里查看答案。

遵循上述规则，我们有I和J作为收缩维度，K、L、M、N和O作为非收缩维度。我们没有“批处理维度”，所以这只是 \(2 \cdot I \cdot J \cdot K \cdot L \cdot M \cdot N \cdot O\)，即所有轴的乘积之和。如果我们有一个共享轴，它只会被计算一次。

问题4： 自注意力的算术强度是多少（忽略Q/K/V/O投影）？以Q和KV长度T和S的函数形式给出答案。 在什么上下文长度下，注意力是FLOPs受限的？给定我们TPU的HBM带宽，绘制随着上下文长度增长，注意力与FFW块的有效相对成本图。

点击这里查看答案。

自注意力需要加载\(Q\)、\(K\)和\(V\)激活，然后计算\(\text{softmax}(Q \cdot K) \cdot V\)，然后将结果写回HBM。这将使用Flash Attention完成，所以这个数学计算有一些注意事项，但基本上在bf16中，自注意力执行

\[\text{Q[B,T,N,H]} \rightarrow_\text{reshape} \text{Q[B, T, K, G, H]} \cdot \text{K[B, S, K, H]} \rightarrow \text{O[B, T, S, K, G]}\] \[U=\text{softmax}_S(\text{O[B, T, S, K, G]}) \] \[\text{U[B, T, S, K, G]} \cdot \text{V[B, S, K, H]} \rightarrow \text{X[B, T, K, G, H]}\]

所以我们的总字节数是 \(2 * \text{sizeof}(Q) + 2 * \text{sizeof(K or V)} = 4BTNH + 4BSKH = 4BHK * (TG + S)\)，总FLOPs是 \(4BTSNH + O(BTSN)\)，算术强度是 \(4BTSKGH / (4BHK * (TG + S))\)。

所以基本上，在预填充期间，我们有\(S=T\)，所以我们的算术强度是\(4BT^2KGH / 4BHKT \cdot (G+1) = TG/(G + 1) = O(T)\)。在生成期间，\(T=1\)，所以我们有\(4BSKGH / (4BHK \cdot (G + S)) = SG / (G + S) \rightarrow G\)，假设\(S\)非常大。根据你如何解释这个问题，在预填充或训练期间，假设没有序列分片，自注意力在S=240时是计算受限的。在生成期间，我们永远不会是计算受限的，因为\(G\)很小。然而，你可以看到，增加\(G\)会使我们更接近计算受限。

问题5： 在什么序列长度下，自注意力的FLOPs等于QKVO投影的FLOPs？

点击这里查看答案。

这纯粹是关于何时\(24BTDNH == 12BT^2NH\)的问题。简化后我们得到\(2D = T\)，例如对于\(D=4096\)，这是\(8192\)。这告诉我们，对于大多数合理的上下文长度，矩阵乘法的FLOPs更大。

问题6： 假设我们在前向传播过程中只保存Transformer层中7个主要矩阵乘法（Q, K, V, O + 三个FFW矩阵）的输出。在反向传播过程中，我们需要“重新物化”多少额外的FLOPs？

点击这里查看答案。

只保存七个矩阵乘法的输出（Q, K, V, O, W₁, W₂, W₃）意味着反向传播必须重新计算两个注意力矩阵乘法

\[QK^{\top} \quad\text{和}\quad \operatorname{softmax}(QK^{\top})V.\]

每个都是在\(B\)个序列和\(N\)个头上批处理的\(T \times T\)矩阵乘法，所以额外的FLOPs是

\[4 \; B \, T^{2} \, N \, H.\]

所有其他重新计算的操作都只是\(O(BTD)\)。

问题7： DeepSeek v3声称它在14.8T个token上训练了279万H800小时（来源）。鉴于它有37B个激活参数，他们大致达到了什么样的硬件利用率？提示：注意他们使用了没有结构化稀疏性的FP8 FLOPs。

点击这里查看答案。

从规格表这里，我们发现带稀疏性的FP8性能为3,026 TFLOPs/s，或者通常不带稀疏性时是这个值的一半（1.513e15 FLOPs/s）。279万H800小时意味着2.79e6 * 1.513e15 * 60 * 60 = 1.52e25总FLOPs。鉴于激活参数数量为37B，这次训练运行应该使用了大约6 * 37e9 * 14.8e12 = 3.3e24 FLOPs。这意味着FLOPs利用率大约是3.3e24 / 1.52e25 = 21.7%。

问题8： 专家混合（MoE）模型有\(E\)个标准密集MLP块的副本，每个token激活其中\(k\)个专家。在TPU v5e上，对于权重为int8的MoE，需要多大的批大小（以token为单位）才能达到计算受限？对于有256个（路由）专家且\(k=8\)的DeepSeek，这个数字是多少？

点击这里查看答案。

因为我们有\(E\)个每个专家的副本，在int8中，我们需要加载\(E \cdot D \cdot F\)字节。因为每个token激活\(k\)个专家，我们有\(2\cdot k \cdot B \cdot D \cdot F\) FLOPs。要使用bfloat16 FLOPs达到计算受限，我们需要算术强度超过240，这发生在\((2\cdot k \cdot BDF) / EDF > 240\)或\(k \cdot B / E > 120\)时。

因此，我们需要\(B > 120 \cdot E / k\)才能达到计算受限。对于DeepSeek，这给我们\(B > 120 \cdot 256 / 8 = 3840\)。这在生成时是一个非常大的批大小。

第4部分到此结束！关于第5部分（扩展Transformer训练），请点击这里！

附录

附录A：Flash Attention是如何工作的？

将Transformer扩展到非常长的上下文的传统反对意见是，注意力的FLOPs和内存使用量随上下文长度呈二次方增长。虽然注意力QK乘积的形状确实是[B, S, T, N]（其中B是批大小，S和T是Q和K的序列维度，N是头的数量），但这一说法带有一些重要的注意事项：

  1. 正如我们在第4节中指出的，即使这是二次方的，注意力的FLOPs也只有在\(S > 8 \cdot D\)时才占主导地位，特别是在训练期间，单个注意力矩阵的内存与内存中存在的所有权重和激活检查点相比是很小的，尤其是在分片的情况下。
  2. 我们不需要为了计算注意力而物化整个注意力矩阵！我们可以计算局部和与最大值，从而避免物化超过一小块数组。虽然总FLOPs仍然是二次方的，但我们大大减少了内存压力。

这第二个观察首先由Rabe等人于2021年提出，后来在Flash Attention论文（Dao等人，2022年）中再次提出。基本思想是将K/V分块计算注意力，我们计算局部的softmax和一些辅助统计数据，然后将它们传递给下一个块，后者将其与自己的局部分块结合起来。具体来说，我们计算

  1. M： \(q \cdot k\)在序列维度上的运行最大值
  2. O： 在序列维度上的运行完整注意力softmax
  3. L： 运行分母\(\sum_i (q \cdot k_i - \text{running max})\)

有了这些，我们只需恒定的内存量就可以计算出新的最大值、新的运行总和和新的输出。为了粗略地描述这是如何工作的，注意力大致是这个操作：

\[\text{Attn}(Q, K, V) = \sum_i \frac{\exp(Q \cdot K_i - \max_j Q \cdot K_j) V_i}{\sum_l \exp(Q \cdot K_l - \max_j Q \cdot K_j)}\]

减去最大值是为了数值稳定性，并且可以在不影响结果的情况下添加，因为\(\sum_i \exp(a_i + b) = \exp(b) \sum \exp(a)\)。只看上面的分母，如果我们想象有两个连续的键向量块，\(K^1\)和\(K^2\)，并且我们为每个块计算局部softmax和\(L^1\)和\(L^2\)

\[L^1 = \sum_i \exp(Q \cdot K_i^1 - \max_j Q \cdot K_j^1)\] \[L^2 = \sum_i \exp(Q \cdot K_i^2 - \max_j Q \cdot K_j^2)\]

然后我们可以通过使用以下公式将它们组合成这两个块的完整softmax和

\[L^\text{combined} = \exp(M^1 - \max(M^1, M^2)) \cdot L^1 + \exp(M^2 - \max(M^1, M^2)) \cdot L^2\]

其中

\[M^1 = \max_j Q \cdot K_j^1 \text{ and } M^2 = \max_j Q \cdot K_j^2\]

这也可以对整个softmax进行，为我们提供了一种累积任意大softmax和的方法。以下是Flash Attention论文中的完整算法。

从硬件的角度来看，这使我们能够将Q的块放入VMEM（上述算法称之为片上SRAM），因此我们只需在每次迭代时加载KV块，从而降低了算术强度。我们也可以将运行统计信息保存在VMEM中。

最后一个值得强调的微妙点是注意力softmax的一个属性，它被用来使Flash VJP（反向模式导数）计算在训练中变得可行。如果我们定义一个中间softmax数组为：

\[S_{ij} = \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_j}}\]

在注意力中，我们从反向模式的dO和V数组中获得dS：

\[dS_{ij} = dO_{id} \cdot_d V_{jd} = \sum_d dO_{id} V_{jd}\]

在将此梯度反向传播到Q和K的过程中

\[d(q_i \cdot k_j) = (dS_{ij} - S_{ij} \cdot_j dS_{ij}) S_{ij}\]

我们利用一个恒等式，它允许我们将沿大键长度维度的收缩与沿特征深度维度的局部收缩进行交换。

\[\begin{align*} S_{ij} \cdot_j dS_{ij} &= \sum_j \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_k}} \sum_d dO_{id} V_{jd} \\ &= \sum_d dO_{id} \sum_j \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_k}} V_{jd} \\ &= \sum_d dO_{id} O_{id} \\ &= dO_{id} \cdot_d O_{id} \end{align*}\]

这种替换对于能够为VJP实现序列块局部计算至关重要，并使得更智能的分片方案（如环形注意力）成为可能。

脚注

  1. 严格来说，这只在我们沿专家所在的同一轴进行数据或序列分片时才会发生。[↩]

参考文献

  1. GLU Variants Improve Transformer
    Shazeer, N., 2020. arXiv [cs.LG].
  2. Fast Transformer decoding: One write-head is all you need
    Noam, S., 2019. arXiv [cs.NE].
  3. GQA: Training generalized multi-query transformer models from multi-head checkpoints
    Ainslie, J., Lee-Thorp, J., de Jong, M., Zemlyanskiy, Y., Lebrón, F. and Sanghai, S., 2023. arXiv [cs.CL].
  4. Outrageously large neural networks: The Sparsely-Gated Mixture-of-experts layer
    Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G. and Dean, J., 2017. arXiv [cs.LG].

其他

*在Google DeepMind工作，现就职于MatX。

引用

在学术背景下引用，请按如下方式引用本作品：

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

或作为BibTeX条目：

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }