 微信公众号
微信公众号
如何为训练并行化Transformer
《如何扩展你的模型》第5部分 (第4部分:Transformer | 第6部分:训练LLaMA)
在这里,我们讨论LLM训练中使用的四种主要并行方案:数据并行、完全分片数据并行(FSDP)、张量并行和流水线并行。对于每一种方案,我们都会计算在何种情况下会受到通信的瓶颈限制。
我们所说的扩展是什么意思?
“模型扩展”的目标是能够增加用于训练或推理的芯片数量,同时实现吞吐量的成比例线性增长(我们称之为强扩展)。虽然单个芯片的性能取决于内存带宽和FLOPs之间的权衡,但集群级别的性能则取决于通过将芯片间通信与有用的FLOPS重叠来隐藏它。这并非易事,因为增加芯片数量会增加通信负载,同时减少了可用于隐藏通信的每设备计算量。正如我们在第3节中看到的,分片的矩阵乘法通常需要昂贵的AllGather或ReduceScatter操作,这些操作可能会阻塞TPU执行有用的工作。本节的目标是找出这些操作在何时会变得过于昂贵。
在本节中,我们将讨论四种常见的并行方案:(纯)数据并行、完全分片数据并行(FSDP / ZeRO分片)、张量并行(也称为模型并行),以及(简要地)流水线并行。对于每一种方案,我们将展示其产生的通信成本,以及该成本在何种情况下开始成为我们计算成本的瓶颈。
在整个本节中,我们将使用以下符号来简化计算。
| 符号 | 含义(模型参数) |
|---|---|
| D | dmodel(隐藏维度/残差流维度) |
| F | dff(前馈维度) |
| B | 批次维度(批次中的token数量;总数,非每设备) |
| T | 序列长度 |
| L | 模型中的层数 |
| 符号 | 含义(硬件特性) |
|---|---|
| C | 每芯片的FLOPs/秒 |
| W | 网络带宽(双向,通常用下标表示,例如 |
| X | 沿网格轴X的芯片数量 |
| Y | 沿备用网格轴Y的芯片数量 |
| Z | 沿第三个网格轴Z的芯片数量 |
为简单起见,我们将把Transformer近似为MLP块的堆栈——正如我们在第4节中看到的,对于较大的模型,注意力机制只占FLOPs中相对较小的一部分。我们还将忽略门控矩阵乘法,从而为每层留下以下简单的结构:
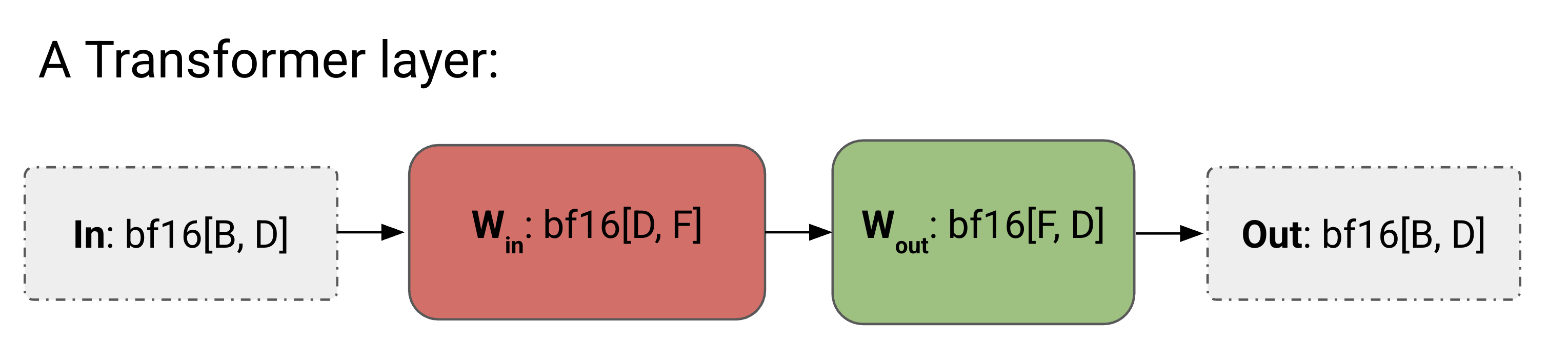
bf16[D, F](上投影)和Wout: bf16[F, D](下投影),输入为In: bf16[B, D]。这是我们没有并行性的小型Transformer的完整算法。
前向传播:需要计算 Loss[B]
- Tmp[B, F] = In[B, D] *D Win[D, F]
- Out[B, D] = Tmp[B, F] *F Wout[F, D]
- Loss[B] = …
反向传播:需要计算 dWout[F, D], dWin[D, F]
- dOut[B, D] = …
- dWout[F, D] = Tmp[B, F] *B dOut[B, D]
- dTmp[B, F] = dOut[B, D] *D Wout[F, D]
- dWin[D, F] = In[B, D] *B dTmp[B, F]
- dIn[B, D] = dTmp[B, F] *F Win[D, F] (后续层需要)
我们提供此算法,以便与添加了通信的算法进行比较。
以下是我们即将讨论的4种并行方案。每种方案都可以被认为是由上图中In、Win、Wout和Out的分片方式唯一确定的。
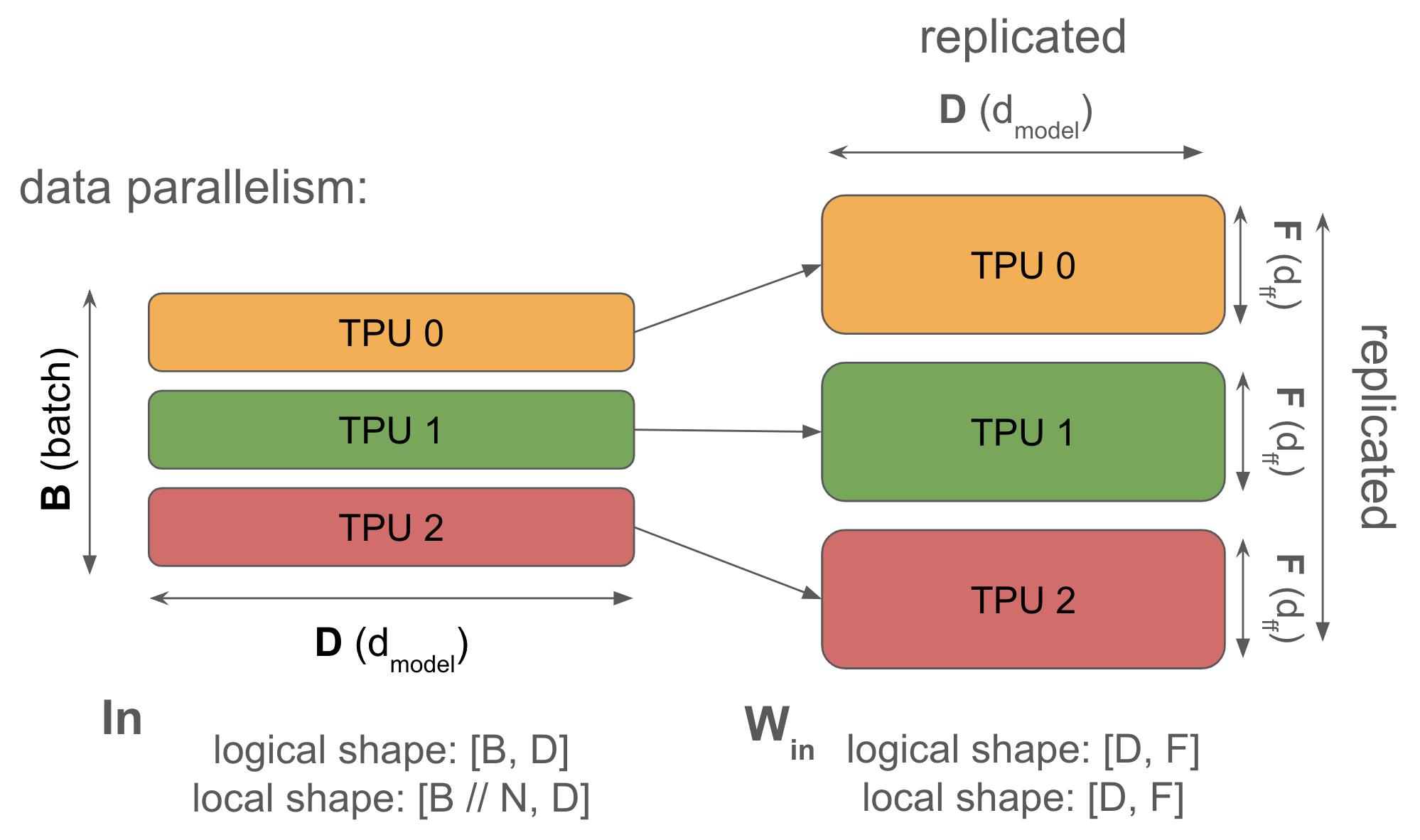
1. 数据并行:激活值沿批次维度分片,参数和优化器状态在每个设备上复制。通信仅在反向传播期间发生。
2. 完全分片数据并行 (FSDP or ZeRO-3):激活值沿批次维度分片(类似于纯数据并行),参数沿相同的网格轴分片,并在前向传播中使用前即时进行AllGather。优化器状态也沿批次维度分片。减少了内存复制。
3. 张量并行(也称为Megatron分片或模型并行):激活值沿D(
4. 流水线并行:权重沿层维度分片,激活值进行微批处理并沿层维度滚动。流水线阶段之间的通信量极小(仅在单个跳跃上传输激活值)。滥用一下符号表示:
数据并行
语法:
当你的模型即使在极小的批次大小(>240个token,以达到计算密集)下也能装入单个芯片时,你应该始终使用简单的数据并行。纯数据并行将我们的激活值分散到任意数量的TPU上,只要TPU的数量小于我们的批次大小。前向传播不涉及通信,但在每一步结束时,每个TPU都会对其本地梯度执行一次AllReduce,以便在更新参数之前同步它们。
这是前向和反向传播的完整算法。我们滥用符号,将dL/dOut写作dOut,纯粹是为了简洁。
纯数据并行算法:
前向传播:需要计算 Loss[BX]
- Tmp[BX, F] = In[BX, D] *D Win[D, F]
- Out[BX, D] = Tmp[BX, F] *F Wout[F, D]
- Loss[BX] = …
反向传播:需要计算 dWout[F, D], dWin[D, F]
- dOut[BX, D] = …
- dWout[F, D] {UX} = Tmp[BX, F] *B dOut[BX, D]
- dWout[F, D] = AllReduce(dWout[F, D] {UX}) (不在关键路径上,可以异步完成)
- dTmp[BX, F] = dOut[BX, D] *D Wout[F, D]
- dWin[D, F] {UX} = In[BX, D] *B dTmp[BX, F]
- dWin[D, F] = AllReduce(dWin[D, F] {UX}) (不在关键路径上,可以异步完成)
- dIn[BX, D] = dTmp[BX, F] *F Win[D, F] (后续层需要)
我们忽略损失函数的细节,并将
请注意,前向传播没有通信——通信都在反向传播中!反向传播还有一个很好的特性,即AllReduce操作不在“关键路径”上,这意味着每个AllReduce都可以在方便的时候执行,而不会阻塞后续操作。如果总通信成本超过了总计算成本,它仍然可能成为我们的瓶颈,但从实现的角度来看,它要宽容得多。我们将看到模型/张量并行不具备此特性。
为什么要这样做?纯数据并行通过沿批次维度分割我们的激活值来减轻激活值内存压力,只要我们有更多的芯片来分割批次维度,我们几乎可以任意增加批次大小。特别是在训练期间,当我们的激活值通常主导内存使用时,这非常有用。
为什么不这样做?纯数据并行对减轻模型参数或优化器状态的内存压力毫无作用,这意味着对于参数+优化器状态无法装入单个TPU的大规模有趣模型,纯数据并行很少有用。为了给出一个规模感,如果我们使用Adam以bf16精度训练参数,以fp32精度存储优化器状态
要点:使用Adam和纯数据并行,我们能训练的最大模型有
为了使其在训练实际模型时有用,我们至少需要部分地对模型参数或优化器进行分片。
我们何时会受到通信瓶颈的限制?如上所示,每层我们有两个AllReduce操作,每个的大小为
如上表所示,设
通信时间:从前一节我们知道,在一维网格中执行AllReduce所需的时间仅取决于被AllReduce的数组的总字节数和ICI带宽
矩阵乘法时间:每层在前向传播中包含两次矩阵乘法,在反向传播中包含四次,每次需要
由于我们进行了重叠,每层的总时间是这两个量的最大值:
当
结论是,为了在使用数据并行时保持计算密集,我们需要每设备批次大小
让我们代入一些真实数字来获得一个规模感。对于TPUv5p,C=4.6e14且W=2 * 9e10(对于ICI上的1D数据并行),所以我们每个芯片的批次大小必须至少为2,550,以避免受限于通信。由于我们可以在多个轴上进行数据并行,如果我们将TPUv5p pod的所有三个轴都用于纯数据并行,我们的带宽
注意[上下文并行]:在本节中,
完全分片数据并行 (FSDP)
语法:
完全分片数据并行(通常称为FSDP或ZeRO分片
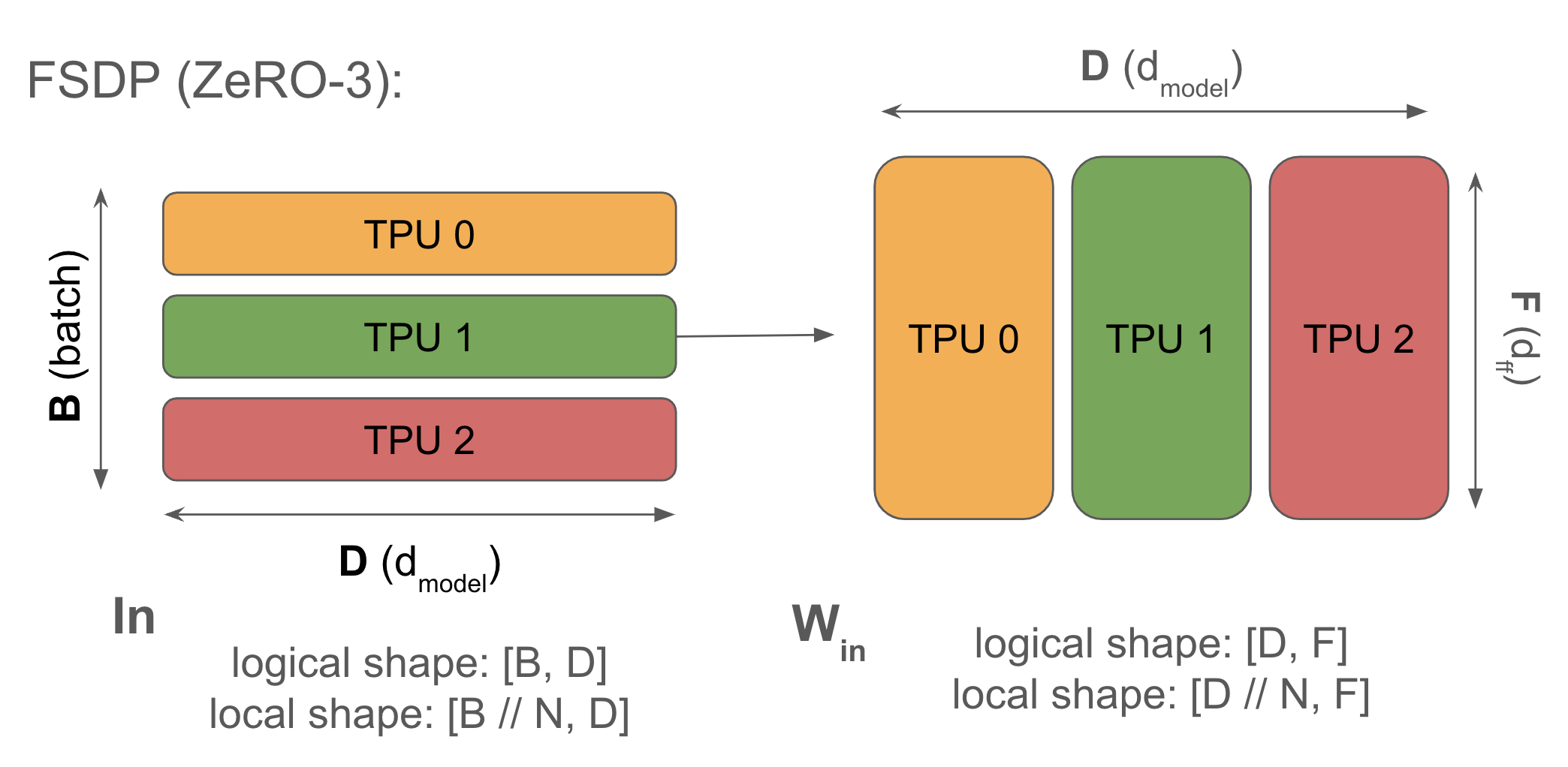
你会记得(从第3节),一个AllReduce可以分解为一个AllGather和一个ReduceScatter。这意味着,我们可以不对标准数据并行执行完整的梯度AllReduce,而是将权重和优化器状态分片到各个芯片上,在前向传播的每一层对它们进行AllGather,并在反向传播期间对权重进行ReduceScatter,而无需额外成本。
这是FSDP的完整算法。
完全分片数据并行 (FSDP):
前向传播:需要计算 Loss[BX]
- Win[D, F] = AllGather(Win[DX, F]) (不在关键路径上,可以在前一层期间完成)
- Tmp[BX, F] = In[BX, D] *D Win[D, F] (现在可以丢弃Win[D, F]了)
- Wout[F, D] = AllGather(Wout[F, DX]) (不在关键路径上,可以在前一层期间完成)
- Out[BX, D] = Tmp[BX, F] *F Wout[F, D]
- Loss[BX] = …
反向传播:需要计算 dWout[F, DX], dWin[DX, F]
- dOut[BX, D] = …
- dWout[F, D] {UX} = Tmp[BX, F] *B dOut[BX, D]
- dWout[F, DX] = ReduceScatter(dWout[F, D] {UX}) (不在关键路径上,可以异步完成)
- Wout[F, D] = AllGather(Wout[F, DX]) (可以提前完成)
- dTmp[BX, F] = dOut[BX, D] *D Wout[F, D] (可以在这里丢弃Wout[F, D])
- dWin[D,F] {UX} = dTmp[BX, F] *B In[BX, D]
- dWin[DX, F] = ReduceScatter(dWin[D, F] {UX}) (不在关键路径上,可以异步完成)
- Win[D, F] = AllGather(Win[DX, F]) (可以提前完成)
- dIn[BX, D] = dTmp[BX, F] *F Win[D, F] (后续层需要) (可以在这里丢弃Win[D, F])
这也被称为“ZeRO分片”,源于“零开销分片(ZeRo Overhead sharding)”,因为我们不执行任何不必要的计算或存储任何不必要的状态。ZeRO-{1,2,3}分别用于指代以这种方式对优化器状态、梯度和权重进行分片。由于所有的通信成本都相同
我们为什么要这样做?标准数据并行涉及大量重复工作。每个TPU都对完整的梯度进行AllReduce,然后更新完整的优化器状态(所有TPU上的工作都相同),接着更新参数(同样是完全重复的)。对于ZeRO分片(对梯度/优化器状态进行分片),你可以ReduceScatter梯度,而不是进行AllReduce,只更新你自己的优化器状态分片,更新一个参数分片,然后在前向传播中根据需要AllGather参数。
我们何时会受到通信瓶颈的限制?我们相对的FLOPs和通信成本与纯数据并行完全相同,因为反向传播中的每个AllReduce都变成了一个AllGather + ReduceScatter。回想一下,AllReduce是作为AllGather和ReduceScatter实现的,每个的成本是其一半。这里我们对前向传播进行建模,因为它与反向传播具有相同的FLOPs与通信比率:
因此,与纯数据并行一样,当4.59e14 / 1.8e11 = 2550)时。这对我们来说非常好,因为这意味着如果我们的每设备批次大小足够大,以至于对于纯数据并行是计算密集的,我们就可以——不用担心离开计算密集区域——简单地升级到FSDP,从而为我们节省大量的参数和优化器状态内存!虽然我们确实必须在前向传播中增加通信,但这个成本是无关紧要的,因为它只是与前向传播的FLOPs重叠。
要点:当每设备批次大小小于
例如,DeepSeek-V2(近期唯一一个公布其训练批次大小信息的强大模型)使用了约4000万token的批次大小。这将允许我们在达到带宽限制之前扩展到大约47,000个芯片,即大约5个TPUv5 pod。
对于LLaMA-3 70B,它经过大约6.3e24 (15e12 * 70e9 * 6) FLOPs的训练,我们可以将1600万token的批次分散到大约16e6 / (2550 / 3) = 18,823个芯片上(大约2个8960芯片的pod),每个芯片的FLOPs为4.59e14,运行在50%的峰值FLOPs利用率(通常称为MFU),并且大约在17天内完成训练。还不错!但让我们探索一下如何做得更好。
关于临界批次大小的说明:有点违反直觉的是,随着总批次大小的减小(芯片数量固定),我们更容易受到通信瓶颈的限制。数据并行和FSDP让我们能够扩展到任意数量的芯片,只要我们能不断增加批次大小!然而,在实践中,随着批次大小的增加,我们往往会看到训练收益递减,因为梯度变得几乎没有噪声。我们有时还会看到训练不稳定的情况。因此,在“无限计算”的情况下寻找最优分片方案的游戏,通常从一个由扩展定律确定的固定批次大小和一个已知(大量)的芯片数量开始,然后旨在找到一种分区方式,以便将那个小批次大小适配到如此多的芯片上。
张量并行
语法:
在完全分片的数据并行AllReduce中,我们在芯片之间移动权重。我们也可以对模型的前馈维度进行分片,并在层内移动激活值——这被称为“1D模型并行”或Megatron分片
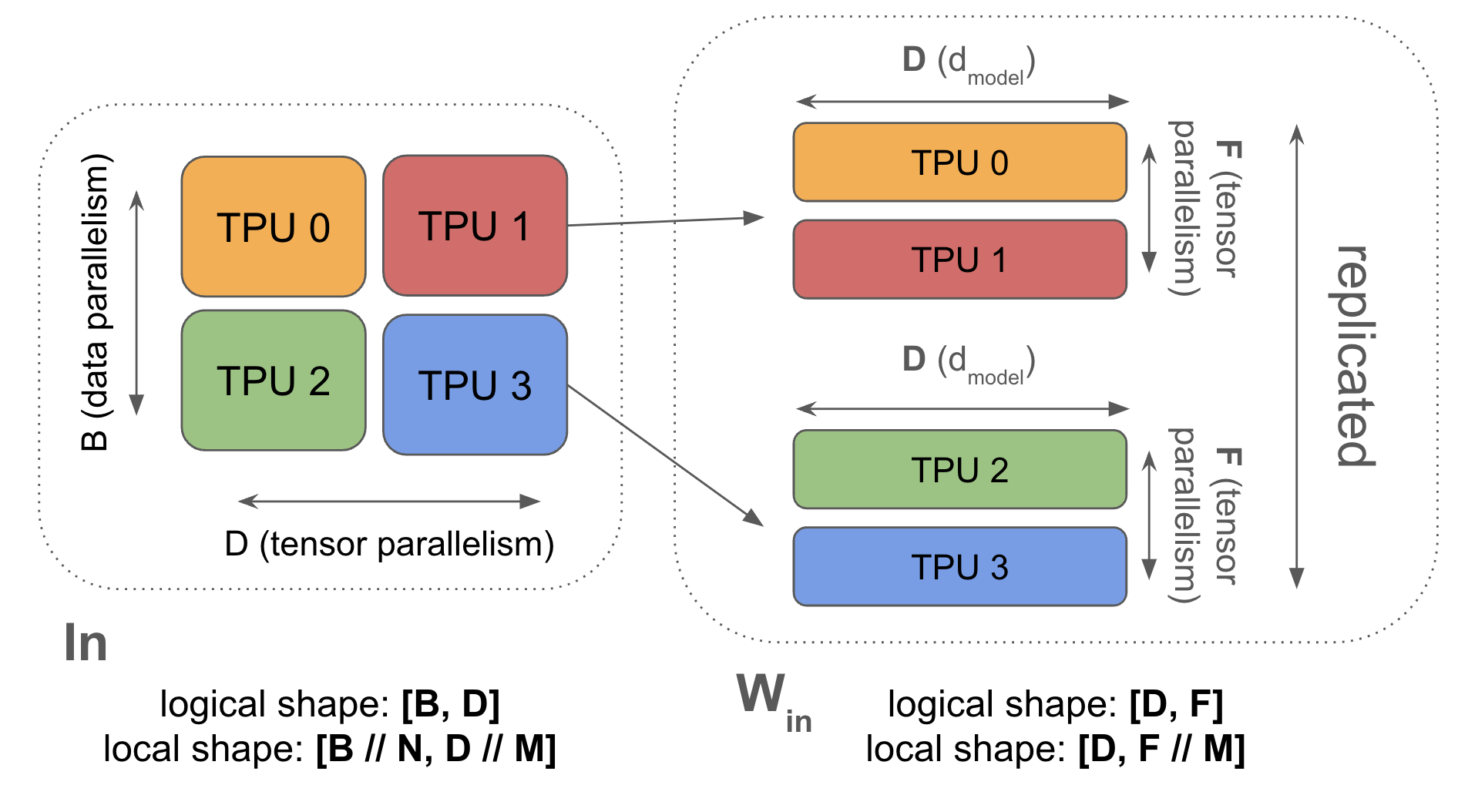
如前所述,In[B, DY] *D Win[D, FY] *F Wout[FY, D] -> Out[B, DY] 意味着我们必须在第一次矩阵乘法前收集我们的激活值。当激活值小于权重时,这比ZeRO分片更便宜。这通常只有在添加了某种程度的ZeRO分片(这会减少收集的大小)时才成立。这是我们倾向于混合使用ZeRO分片和张量并行的原因之一。
这是张量并行的算法!
张量并行:
前向传播:需要计算 Loss[B]
- In[B, D] = AllGather(In[B, DY]) (在关键路径上)
- Tmp[B, FY] = In[B, D] *D Win[D, FY] (未沿收缩维度分片,因此无通信)
- Out[B, D] {UY} = Tmp[B, FY] *F Wout[FY, D]
- Out[B, DY] = ReduceScatter(Out[B, D] {UY}) (在关键路径上)
- Loss[B] = …
反向传播:需要计算 dWout[FY, D], dWin[D, FY]
- dOut[B, DY] = …
- dOut[B, D] = AllGather(dOut[B, DY]) (在关键路径上)
- dWout[FY, D] = Tmp[B, FY] *B dOut[B, D]
- dTmp[B, FY] = dOut[B, D] *D Wout[FY, D] (可以在这里丢弃dOut[B, D])
- In[B, D] = AllGather(In[B, DY]) (这可以通过与前向传播的(1)共享来跳过)
- dWin[D, FY] = dTmp[B, FY] *B In[B, D]
- dIn[B, D] {U.Y} = dTmp[B, FY] *F Win[D, FY] (后续层需要)
- dIn[B, DY] = ReduceScatter(dIn[B, D] {U.Y}) (在关键路径上)
张量并行的一个好处是它与我们Transformer前向传播中的两个矩阵很好地交互。天真地看,我们会在每个矩阵后都做一个AllReduce。但在这里,我们首先做In[B, DY] * Win[D, FY] -> Tmp[B, FY],然后是Tmp[B, FY] * Wout[FY, D] -> Out[B, DY]。这意味着我们在开始时对In进行AllGather,在结束时对Out进行ReduceScatter,而不是做一个AllReduce。
这有多昂贵?我们只对前向传播进行建模——反向传播只是这里每个操作的转置。在1D张量并行中,我们在第一次矩阵乘法前对激活值进行AllGather,在第二次之后进行ReduceScatter,每次发送两个字节(bf16)。让我们计算一下我们何时会受到通信瓶颈的限制。
注意到我们希望计算成本大于通信成本,我们得到:
因此,例如,对于TPUv5p,在bf16中
要点:当
请注意,这不依赖于计算的精度,例如,对于int8,在TPUv5p上,
让我们考虑一些例子:
-
在TPUv5p上使用LLaMA 3-70B,其中
-
对于Gemma 7B,
结合FSDP和张量并行
语法:
FSDP和张量并行的好处在于它们可以结合使用。通过在两个轴上对Win和Wout进行分片,我们既节省了内存又节省了计算。因为我们在X轴上对B进行分片,我们减小了模型并行AllGather的大小;因为我们在Y轴上对F进行分片,我们减少了FSDP的通信开销。这意味着两者的结合可以让我们达到比上面看到的更低的有效批次大小。

这是混合FSDP+张量并行的完整算法。虽然我们有很多通信,但我们所有的AllGather和ReduceScatter都更小,因为我们对激活值进行了批次分片,并对权重进行了更多的张量分片!
前向传播:需要计算 Loss[B]
- In[BX, D] = AllGatherY(In[BX, DY]) (在关键路径上)
- Win[D, FY] = AllGatherX(Win[DX, FY]) (可以提前完成)
- Tmp[BX, FY] = In[BX, D] *D Win[D, FY]
- Wout[FY, D] = AllGatherX(Wout[FY, DX]) (可以提前完成)
- Out[BX, D] {U.Y} = Tmp[BX, FY] *F Wout[FY, D]
- Out[BX, DY] = ReduceScatterY(Out[BX, D] {U.Y}) (在关键路径上)
- Loss[BX] = …
反向传播:需要计算 dWout[FY, DX], dWin[DX, FY]
- dOut[BX, DY] = …
- dOut[BX, D] = AllGatherY(dOut[BX, DY]) (在关键路径上)
- dWout[FY, D] {U.X} = Tmp[BX, FY] *B dOut[BX, D]
- dWout[FY, DX] = ReduceScatterX(dWout[FY, D] {U.X})
- Wout[FY, D] = AllGatherX(Wout[FY, DX]) (可以提前完成)
- dTmp[BX, FY] = dOut[BX, D] *D Wout[FY, D] (可以在这里丢弃dOut[B, D])
- In[BX, D] = AllGatherY(In[BX, DY]) (不在关键路径上 + 这可以与前一层的(2)共享)
- dWin[D, FY] {U.X} = dTmp[BX, FY] *B In[BX, D]
- dWin[DX, FY] = ReduceScatterX(dWin[D, FY] {U.X})
- Win[D, FY] = AllGatherX(Win[DX, FY]) (可以提前完成)
- dIn[BX, D] {U.Y} = dTmp[BX, FY] *F Win[D, FY] (后续层需要)
- dIn[BX, DY] = ReduceScatterY(dIn[BX, D] {U.Y}) (在关键路径上)
FSDP和TP的正确组合是什么?一个简单但关键的准则是,FSDP移动权重,而张量并行移动激活值。这意味着随着我们的批次大小缩小(特别是在我们进行更多数据并行时),张量并行变得更便宜,因为我们每个分片的激活值更小。
- 张量并行执行
- FSDP执行
因此,通过结合两者,我们可以将每个副本的最小批次大小推得更低。我们可以用与上面相同的方式计算FSDP和TP的最优量:
设
同样,我们的总FLOPs时间是
为了简化分析,我们做两个假设:首先,我们允许
在我们询问在什么条件下我们会是计算密集型之前,让我们先找到
因为
这非常有用!它告诉我们,对于给定的
要点:总的来说,在训练期间,FSDP的最优量是
现在让我们回到我们一直对所有并行策略提出的问题:在什么条件下我们会是计算密集的?由于我们可以重叠FLOPs和通信,当以下条件成立时我们是计算密集的
通过令
由于我们计算了
进一步简化,我们发现
其中左侧与通信时间成正比,右侧与计算时间成正比。请注意,虽然计算时间与批次大小成线性比例(无论采用何种并行性),但通信时间与批次大小的平方根成比例。因此,计算时间与通信时间的比率也与批次大小的平方成比例:
为了确保这个比率大于1,从而我们是计算密集的,我们需要
为了得到近似数字,再次代入
要点:将张量并行与FSDP相结合,使我们能够将
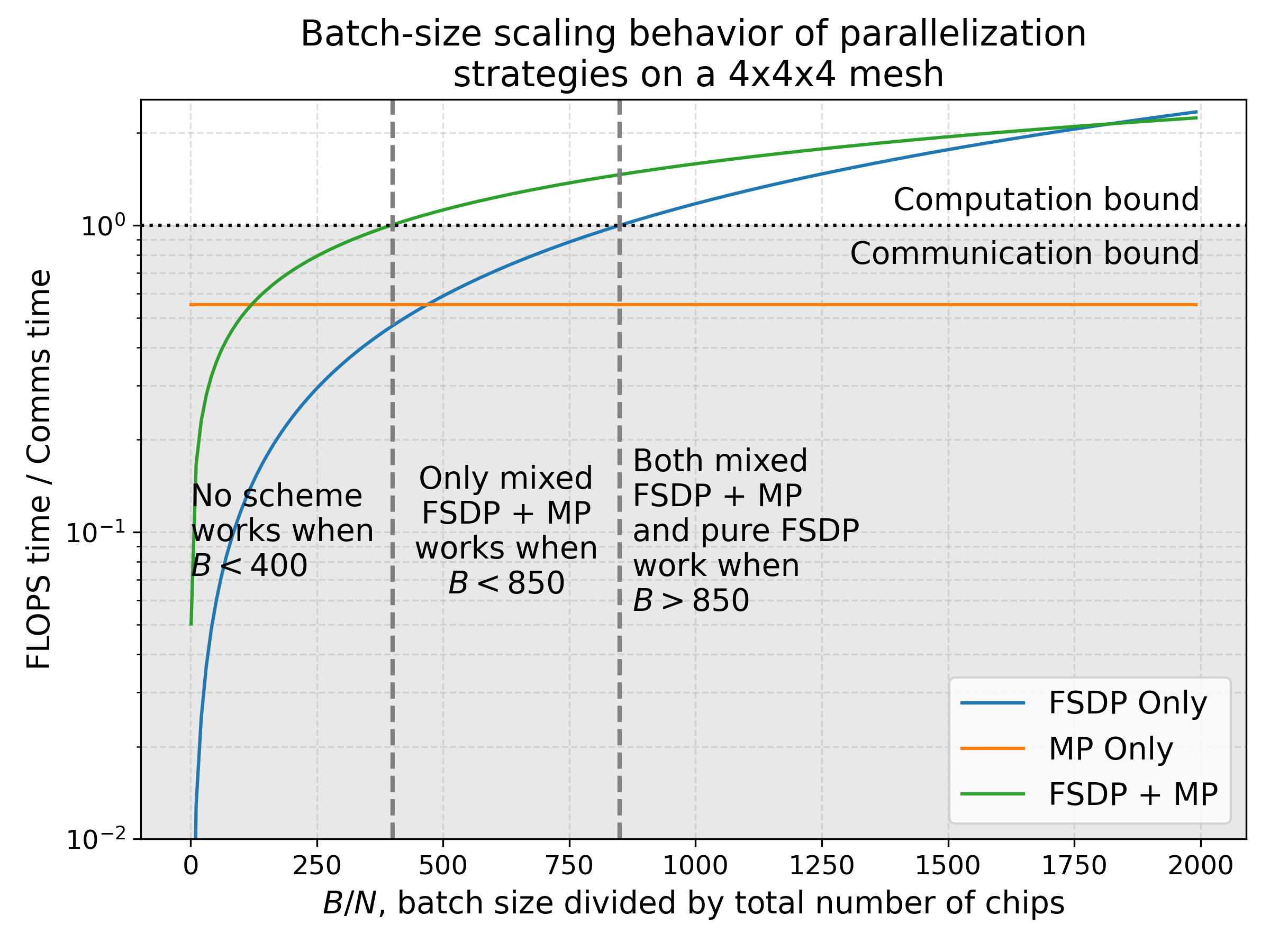
下面我们绘制了混合FSDP+TP的FLOPs与通信时间比率,并将其与仅张量并行(TP)和仅数据并行(FSDP)在代表性的4x4x4芯片阵列上进行比较。虽然纯FSDP并行在非常大的批次大小下占主导地位,但在批次大小与芯片数量之比介于大约100和850之间的区域,需要采用混合FSDP+TP策略才能达到计算密集。
这是另一个TPU v5p 16x16x16的例子,显示了不同分片方案下FLOPs和通信时间随批次大小变化的函数。
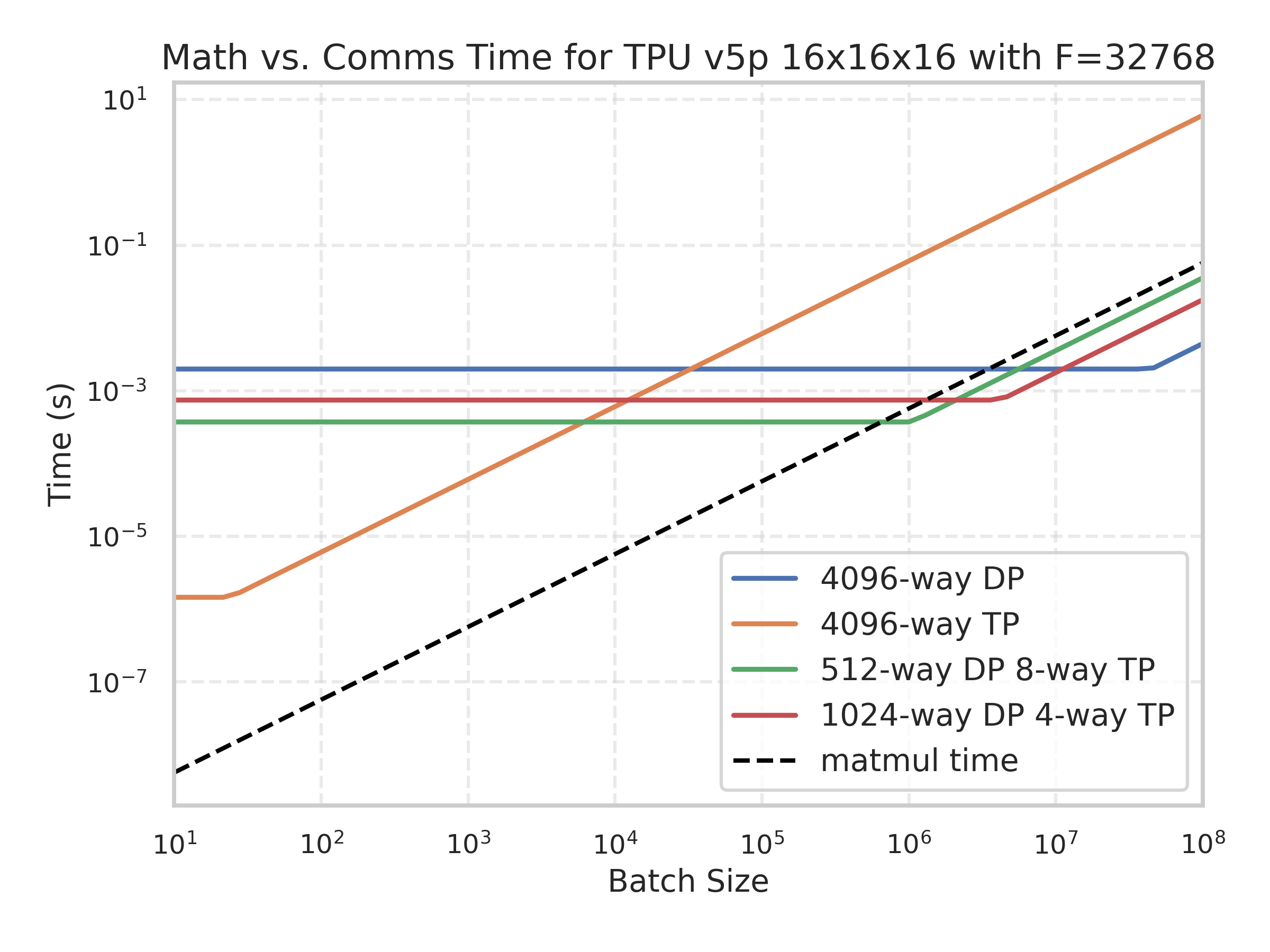
黑色曲线是模型FLOPs所花费的时间,这意味着任何批次大小下,如果这个值低于所有通信成本,那么它就是严格的通信密集型。你会注意到黑色曲线与绿色曲线在大约4e5处相交,正如预测的那样。
这是一个交互式动画,可以让你体验这一点,显示不同批次大小下的总计算时间和通信时间:
你会注意到,这通常与上述结论一致(最小值在FSDP=256,TP=16附近),加上或减去一些微小的波动,因为每个方案的轴数略有不同。
流水线并行
你可能已经注意到,我们在前面的章节中完全没有讨论流水线并行。流水线并行是GPU并行性的一种主导策略,但在TPU上则不那么重要。简而言之,流水线训练涉及将模型的层分散到多个设备上,并在前向和后向传播期间在流水线阶段之间传递激活值。算法大致如下:
- 在TPU 0上初始化你的数据,并将你的权重沿层维度分片(对于带有FSDP和张量并行的流水线,为
W_\text{in}[L_Z, D_X, F_Y] )。 - 在TPU 0上执行第一层,然后将得到的激活值复制到TPU 1,重复此过程直到最后一个TPU。
- 计算损失函数及其导数
\partial L / \partial x_L 。 - 对于最后一个流水线阶段,计算导数
\partial L / \partial W_L 和\partial L / \partial x_{L-1} ,然后将\partial L / \partial x_{L-1} 复制到前一个流水线阶段,重复此过程直到到达TPU 0。
这是一些(可运行的)Python伪代码
这段伪代码应该可以在Cloud TPU VM上运行。虽然它效率不高也不现实,但它能让你了解数据是如何在设备间传播的。
batch_size = 32
d_model = 128
d_ff = 4 * d_model
num_layers = len(jax.devices())
key = jax.random.PRNGKey(0)
# Pretend each layer is just a single matmul.
x = jax.random.normal(key, (batch_size, d_model))
weights = jax.random.normal(key, (num_layers, d_model, d_model))
def layer_fn(x, weight):
return x @ weight
# Assume we have num_layers == num_pipeline_stages
intermediates = [x]
for i in range(num_layers):
x = layer_fn(x, weights[i])
intermediates.append(x)
if i != num_layers - 1:
x = jax.device_put(x, jax.devices()[i+1])
def loss_fn(batch):
return jnp.mean(batch ** 2) # make up some fake loss function
loss, dx = jax.value_and_grad(loss_fn)(x)
for i in range(0, num_layers, -1):
_, f_vjp = jax.vjp(layer_fn, intermediates[i + 1], weights[i])
dx, dw = f_vjp(dx) # compute the jvp dx @ J(L)(x[i], W[i])
weights[i] = weights[i] - 0.01 * dw # update our weights
if i != 0:
dx = jax.device_put(dx, jax.devices()[i-1])
为什么这是个好主意?流水线并行有很多优点:它在流水线阶段之间的通信成本低,这意味着即使在低带宽互连的情况下,你也可以训练非常大的模型。这在GPU上通常非常有用,因为它们不像TPU那样通过ICI密集连接。
为什么这很困难/烦人?你可能已经在上面的伪代码中注意到,TPU 0几乎总是空闲的!它只在流水线的第一个和最后一个步骤中工作。这段空闲时间被称为流水线气泡,处理起来非常烦人。通常我们首先尝试通过微批处理来缓解这个问题,即通过流水线发送多个小批次,从而使TPU 0在总步骤时间的更大部分内保持利用。
第二种方法是仔细重叠前向矩阵乘法

因为它对TPU(拥有更大互连的pod)不那么关键,我们不会深入探讨这一点,但理解关键的流水线瓶颈是一个很好的练习。
跨Pod扩展
最大的TPU切片是TPU v5p SuperPod,拥有8960个芯片(和2240个主机)。当我们想要扩展到这个规模之外时,我们需要跨越数据中心网络(DCN)边界。每个TPU主机都配备了一个或多个NIC(网络接口卡),通过以太网将主机连接到其他TPU v5p pod。正如在TPU部分中提到的,每个主机大约有200Gbps(25GB/s)的全双工DCN带宽,这相当于每个TPU有大约6.25GB/s的全双工(出口)带宽。
通常,当扩展到单个pod之外时,我们在ICI域内进行某种形式的模型并行或FSDP,然后在多个pod之间进行纯数据并行。设
通信带宽随
对于TPU v5p,4.46e14 / 6.25e9 = 71,360。这告诉我们,为了有效地在DCN上扩展,每个ICI域需要一个最小的批次大小才能从每个节点出口。
这有多大问题?举个具体的例子,假设我们想在TPU v5p上用2M tokens的BS训练LLaMA-3 70B。LLaMA-3 70B的
- 我们可以进行张量并行,直到
Y = M_Y \cdot F / 2550 \approxeq 11 \cdot M_Y 。 - 只要
B / N > 2550 / M_X ,我们就可以进行FSDP。这意味着如果我们想用BS=2M和3个数据并行轴进行训练,我们最多只能使用\approx 2400 个芯片,大约是TPU v5p pod的四分之一。 - 当我们结合FSDP+张量并行时,当
B / N < 2550^2 / 2 * 30,000 = 108 时,我们会受到通信限制,所以这让我们能够扩展到大约18k个芯片!然而,TPU v5p pod的最大尺寸是8k个芯片,所以超过这个数量我们就必须使用DCN。
简而言之,我们有一个很好的配方,可以用BS=1M进行训练,大约使用X (FSDP) = 1024和Y (TP) = 8,但对于BS=2M,我们需要使用DCN。如上所述,我们的DCN算术强度为
要点:只要我们每个pod的批次大小至少为71k tokens,使用纯数据并行跨多个TPU pod进行扩展是相当直接的。
在TPU上训练LLM的要点
-
增加并行性或减少批次大小都倾向于使我们更受通信限制,因为它们减少了每个芯片执行的计算量。
-
在合理的上下文长度(~32k)内,我们可以将Transformer建模为MLP块的堆栈,并根据它们如何分片每层的两/三个主要矩阵乘法来定义几种并行方案。
-
在训练期间,我们考虑4种主要的并行方案,每种方案都有其自己的带宽和计算要求(数据并行、FSDP、张量并行)。
| 策略 | 描述 |
|---|---|
| 数据并行 | 激活值按批次分片,其他所有内容完全复制,我们在反向传播期间对梯度进行all-reduce。 |
| FSDP | 激活值、权重和优化器都按批次分片,权重在使用前即时收集,梯度进行reduce-scatter。 |
| 张量并行(又名Megatron、模型并行) | 激活值沿 |
| 混合FSDP+张量并行 | 以上两者的结合,其中FSDP收集模型分片的权重。 |
以下是每种方法的“公式”:
- 这些策略中的每一种都有一个极限,在该极限下它会变得受网络/通信限制,这取决于它们每设备的计算和通信。以下是每层的计算和通信,假设
-
纯数据并行很少有用,因为模型及其优化器状态使用的字节数=10倍参数数量。这意味着我们很少能在内存中容纳超过几十亿个参数。
-
当
-
当
-
混合FSDP+张量并行让我们能够将批次大小降低到
-
跨pod的数据并行要求每个pod的最小批次大小约为75,000,否则会受到DCN的限制。
-
基本上,如果你的批次大小很大或者模型很小,事情就简单了。你可以进行数据并行,或者FSDP+跨DCN的数据并行。中间部分才是事情变得有趣的地方。
一些练习题
让我们使用LLaMA-2 13B作为本节的基本模型。以下是模型细节:
| 超参数 | 值 |
|---|---|
| L | 40 |
| D | 5,120 |
| F | 13824 |
| N | 40 |
| K | 40 |
| H | 128 |
| V | 32,000 |
LLaMA-2有独立的嵌入和输出矩阵以及一个门控MLP块。
问题1:LLaMA-2 13B有多少个参数(我知道这很傻,但请计算一下)?请注意,就像在Transformer数学中一样,LLaMA-3有3个大的FFW矩阵,两个上投影和一个下投影。我们在本节中忽略了两个“门控”einsum矩阵,但它们的行为与本节中的Win相同。
点击此处查看答案。
- FFW参数:
8.5e9 - 注意力参数:
4.2e9 - 词汇表参数:
0.3e9 - 总计:
8.5e9 + 4.2e9 + 0.39e9 = 13.1e9,正如预期!
问题2:假设我们使用BS=16M tokens和Adam进行训练。暂时不考虑并行性,模型的参数、优化器状态和激活值总共使用了多少内存?假设我们以bf16存储参数,以fp32存储优化器状态,并且每层对激活值进行三次检查点(在三个大的矩阵乘法之后)。
点击此处查看答案。
参数(bf16)和两个优化器状态(fp32,一阶和二阶矩累加器)使用的总内存是(2 + 4 + 4) * 13e9 ~ 130GB。前两个矩阵乘法后的激活值形状为2 * 40 * 16e6 * 5,120 * (1 + 2 * 2.7) ~ 4.2e13 = 42TB,因为B=16e16。所有其他激活值或多或少可以忽略不计。
问题3:假设我们想在TPUv5p 16x16x16切片上用32k序列长度和总批次大小3M tokens进行训练。假设我们想使用bfloat16权重和float32优化器,如上所述。
- 我们能使用纯数据并行吗?为什么能或为什么不能?
- 我们能使用纯FSDP吗?为什么能或为什么不能?使用纯FSDP,每个设备将使用多少内存(假设我们只在3个大的FFW矩阵后进行梯度检查点)。
- 我们能使用混合FSDP+张量并行吗?为什么能或为什么不能?如果可以,
X 和Y 应该是什么?每个设备将存储多少内存?仅使用RooflineFLOPs估算并忽略注意力,在40% MFU下每个训练步骤需要多长时间?
点击此处查看答案。
首先,让我们记下一些数字。对于32k序列长度和3M批次大小,我们的序列批次大小是96。在一个TPU v5p 16x16x16切片上,我们有393TB的HBM。
-
我们不能使用纯数据并行,因为它在每个芯片上复制参数和优化器状态,这些已经大约是130GB(来自问题2),这比我们每个芯片的HBM(96GB)要多。
-
让我们先只看内存。将问题2中的BS=16M替换为3M,我们得到
~7.86e12的总检查点激活值,加上1.3e11的优化器状态,这使我们几乎正好达到8e12 = 8TB。TPUv5p切片总共有393TB的HBM,所以我们安全地低于HBM限制。接下来让我们看看我们是会受通信限制还是计算限制。对于4096个芯片和3个并行轴,我们可以做的最小批次大小是850 * 4096 = 3.48Mtokens。这略高于我们的3M批次大小。所以我们实际上是受通信限制的,这很遗憾。所以总的答案是不,我们不能单独使用FSDP。 -
现在我们知道我们的主要担忧是受通信限制,所以让我们代入一些数字。首先,我们从上面知道,我们混合FSDP+张量并行的每芯片批次大小需要高于
2550^2 / 2F = 235 。这意味着理论上我们可以做到!让我们计算一下每种的量。
我们有规则sqrt(3e6 * 2 * 4096 / 13824) = 1333,这意味着我们将大约做1024路DP和4路TP。每个TPU的内存将如(2)所示,步骤时间将是6 * 3e6 * 13e9 / (4096 * 4.6e14 * 0.4) = 300ms。
第5部分到此结束!关于第6部分,它将这些内容应用于真实的LLaMA模型,请点击这里!
附录
附录A:推导反向传播的通信
上面,我们将Transformer层的前向传播简化为Out[B, D] = In[B, D] *D Win[D, F] *F Wout[F, D]。我们如何推导反向传播所需的通信?
这很自然地遵循了前一节中单个矩阵乘法Y = X * A的规则:
使用这个,我们得到以下公式(让Tmp[B, F]代表In[B, D] * Win[D, F]):
- dWout[F, D] = Tmp[B, F] *B dOut[B, D]
- dTmp[B, F] = dOut[B, D] *D Wout[F, D]
- dWin = dTmp[B, F] *B Tmp[B, F]
- dIn[B, D] = dTmp[B, F] *F Win[D, F]
请注意,这些公式是数学陈述,没有提到分片。反向传播的任务是计算这四个量。所以要计算出必要的通信,我们只需取上面四个方程中要进行矩阵乘法的所有量的分片(Tmp, dOut, Wout, Win),这些是由我们的并行化方案指定的,然后使用分片矩阵乘法的规则来计算出我们必须做的通信。请注意,dOut的分片方式与Out相同。
脚注
- 我们将重点关注通信边界——因为虽然内存容量限制很重要,但在预训练期间使用重物质化(激活检查点)和大量芯片时,它们通常不会成为我们的限制因素。我们在此也不讨论用于MoE的专家并行——这极大地扩展了设计空间,我们只讨论密集Transformer的基本情况。[↩]
- Adam存储参数、一阶和二阶累加器。由于参数是bfloat16格式,优化器状态是float32格式,这使得每个参数需要`2 + 8 = 10`字节。[↩]
- 请注意,这不包括梯度检查点,所以这实际上没有用。这是一个批次为1个token时的绝对下限。[↩]
- 我们假设这个分区是在ICI网格上完成的,所以相关的网络带宽是
W_\text{ici} [↩] - 严格来说,FSDP在前向传播中增加了纯DP所没有的通信,但这与反向传播的比例相同,因此它应该对通信Roofline没有影响。关键在于ZeRO-3将反向传播的AllReduce转变为一个AllGather和一个ReduceScatter,它们的总通信量是相同的。[↩]
参考文献
- ZeRO: Memory optimizations toward training Trillion parameter models
Rajbhandari, S., Rasley, J., Ruwase, O. and He, Y., 2019. arXiv [cs.LG]. - Megatron-LM: Training multi-billion parameter language models using model parallelism
Shoeybi, M., Patwary, M., Puri, R., LeGresley, P., Casper, J. and Catanzaro, B., 2019. arXiv [cs.CL]. - DeepSeek-V3 Technical Report
{DeepSeek-AI},, Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Guo, D., Yang, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Zhang, H., Ding, H., Xin, H., Gao, H., Li, H., Qu, H., Cai, J.L., Liang, J., Guo, J., Ni, J., Li, J., Wang, J., Chen, J., Chen, J., Yuan, J., Qiu, J., Li, J., Song, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Xu, L., Xia, L., Zhao, L., Wang, L., Zhang, L., Li, M., Wang, M., Zhang, M., Zhang, M., Tang, M., Li, M., Tian, N., Huang, P., Wang, P., Zhang, P., Wang, Q., Zhu, Q., Chen, Q., Du, Q., Chen, R.J., Jin, R.L., Ge, R., Zhang, R., Pan, R., Wang, R., Xu, R., Zhang, R., Chen, R., Li, S.S., Lu, S., Zhou, S., Chen, S., Wu, S., Ye, S., Ye, S., Ma, S., Wang, S., Zhou, S., Yu, S., Zhou, S., Pan, S., Wang, T., Yun, T., Pei, T., Sun, T., Xiao, W.L., Zeng, W., Zhao, W., An, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Li, X.Q., Jin, X., Wang, X., Bi, X., Liu, X., Wang, X., Shen, X., Chen, X., Zhang, X., Chen, X., Nie, X., Sun, X., Wang, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yu, X., Song, X., Shan, X., Zhou, X., Yang, X., Li, X., Su, X., Lin, X., Li, Y.K., Wang, Y.Q., Wei, Y.X., Zhu, Y.X., Zhang, Y., Xu, Y., Xu, Y., Huang, Y., Li, Y., Zhao, Y., Sun, Y., Li, Y., Wang, Y., Yu, Y., Zheng, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Tang, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Wu, Y., Ou, Y., Zhu, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Zha, Y., Xiong, Y., Ma, Y., Yan, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Wu, Z.F., Ren, Z.Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Huang, Z., Zhang, Z., Xie, Z., Zhang, Z., Hao, Z., Gou, Z., Ma, Z., Yan, Z., Shao, Z., Xu, Z., Wu, Z., Zhang, Z., Li, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Gao, Z. and Pan, Z., 2024. arXiv [cs.CL].