当我们在成千上万个 TPU 或 GPU 上训练一个大语言模型时，我们抽象地进行的计算与在单个设备上训练时是相同的。不同之处在于我们的数组无法装入单个 TPU/GPU 的 HBM，所以我们必须将它们分割开来。值得注意的是，我们可能也会为了速度而选择并行化。即使我们可以将模型装入较少数量的芯片，扩展到更多芯片可以简单地为我们提供更多的 FLOPs/s。例如，在推理期间，我们有时可以装入更小的拓扑结构，但选择扩展到更大的拓扑结构以减少延迟。同样，在训练期间，我们经常扩展到更多的芯片以减少步长时间。我们称之为对数组进行“分片”或“分区”。扩展的艺术在于弄清楚如何对模型进行分片，以保持计算的高效性。

这是一个在 4 个 TPU 上进行分片的 2D 数组 A 的例子：

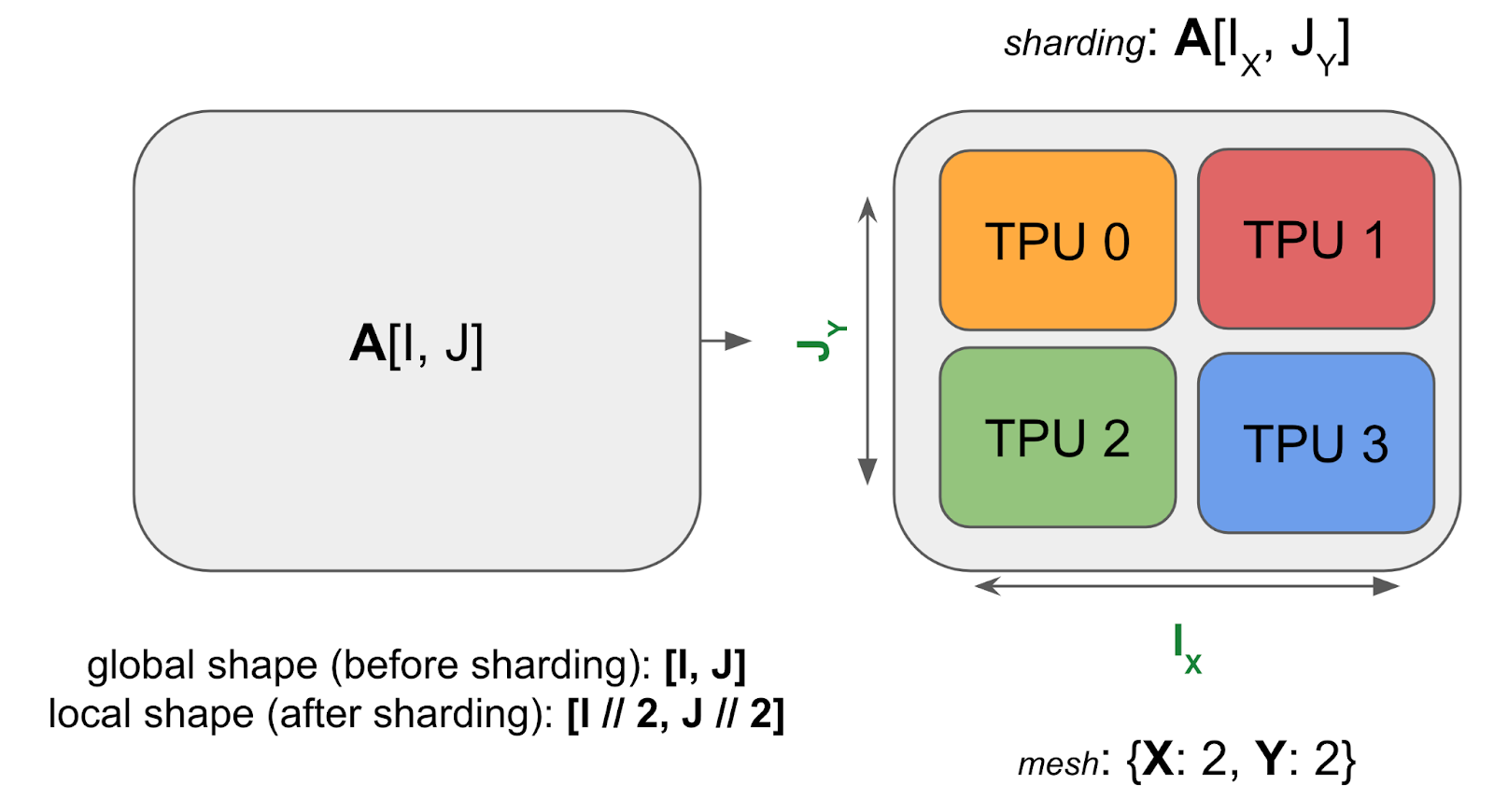
图：一个形状为 A[I, J] 的示例数组被分片到 4 个设备上。两个维度都均匀地分片到 2 个设备上，分片方式为 A[I_X, J_Y]。每个 TPU 持有总内存的 1/4。

注意分片后的数组仍然具有与未分片数组相同的全局或逻辑形状，例如 (4, 128)，但它还有一个设备本地形状，例如 (2, 64)，这告诉我们每个 TPU 实际持有的字节大小（在上图中，每个 TPU 持有总数组的 ¼）。现在我们将这个概念推广到任意数组。

统一的分片表示法

我们使用一种命名轴表示法的变体来描述张量如何以块的形式分片到设备上：我们假设存在一个 2D 或 3D 的设备网格，称为设备网格，其中每个轴都被赋予了网格轴名称，例如 X、Y 和 Z。然后，我们可以通过描述数组的每个命名维度如何跨物理网格轴进行分区来指定矩阵数据在设备网格上的布局。我们将这种分配称为分片。

示例（上图）：对于上图，我们有：

网格：上面的设备网格 Mesh(devices=((0, 1), (2, 3)), axis_names=(‘X', ‘Y'))，它告诉我们有 4 个 TPU 在一个 2x2 的网格中，轴名称为 $X$ 和 $Y$。
分片：$A[I_X, J_Y]$，它告诉我们将第一个轴 $I$ 沿网格轴 $X$ 进行分片，将第二个轴 $J$ 沿网格轴 $Y$ 进行分片。这种分片方式告诉我们，每个分片持有数组的 $1 / (|X| \cdot |Y|)$。

综合来看，我们知道数组的本地形状（单个设备持有的分片大小）是 $(|I| / 2, |J| / 2)$，其中 $| I |$ 是 A 的第一个维度的大小， $| J |$ 是 A 的第二个维度的大小。

小测验 [沿 1 个轴的 2D 分片]：考虑一个数组 fp32[1024, 4096]，其分片方式为 $A[I_{XY}, J]$，设备网格为 {'X': 8, 'Y': 2}。每个设备持有多少数据？在 H100s 上从 HBM 加载这个数组需要多长时间（假设每个芯片的内存带宽为 3.4e12）？

点击此处查看答案。

$A[I_{XY}, J]$ 将第一个维度 (I) 沿 X 和 Y 两个硬件轴进行分片。每个设备的字节数与之前的分片方式相同，但本地形状不同。现在是 $(|I| / (|X| \cdot |Y|), |J|)$。对于给定的例子，全局形状是 fp32[1024, 4096]，所以本地形状是 fp32[64, 4096]。

由于每个 GPU 拥有 4 * 64 * 4096 = 262kB，这大约需要 1e6 / 3.4e12 = 294ns，尽管由于数据量太小，各种开销可能会使其显著增加。

可视化这些分片： 让我们尝试通过观察一个分布在 4 个设备上的 2D 数据数组来可视化这些分片：

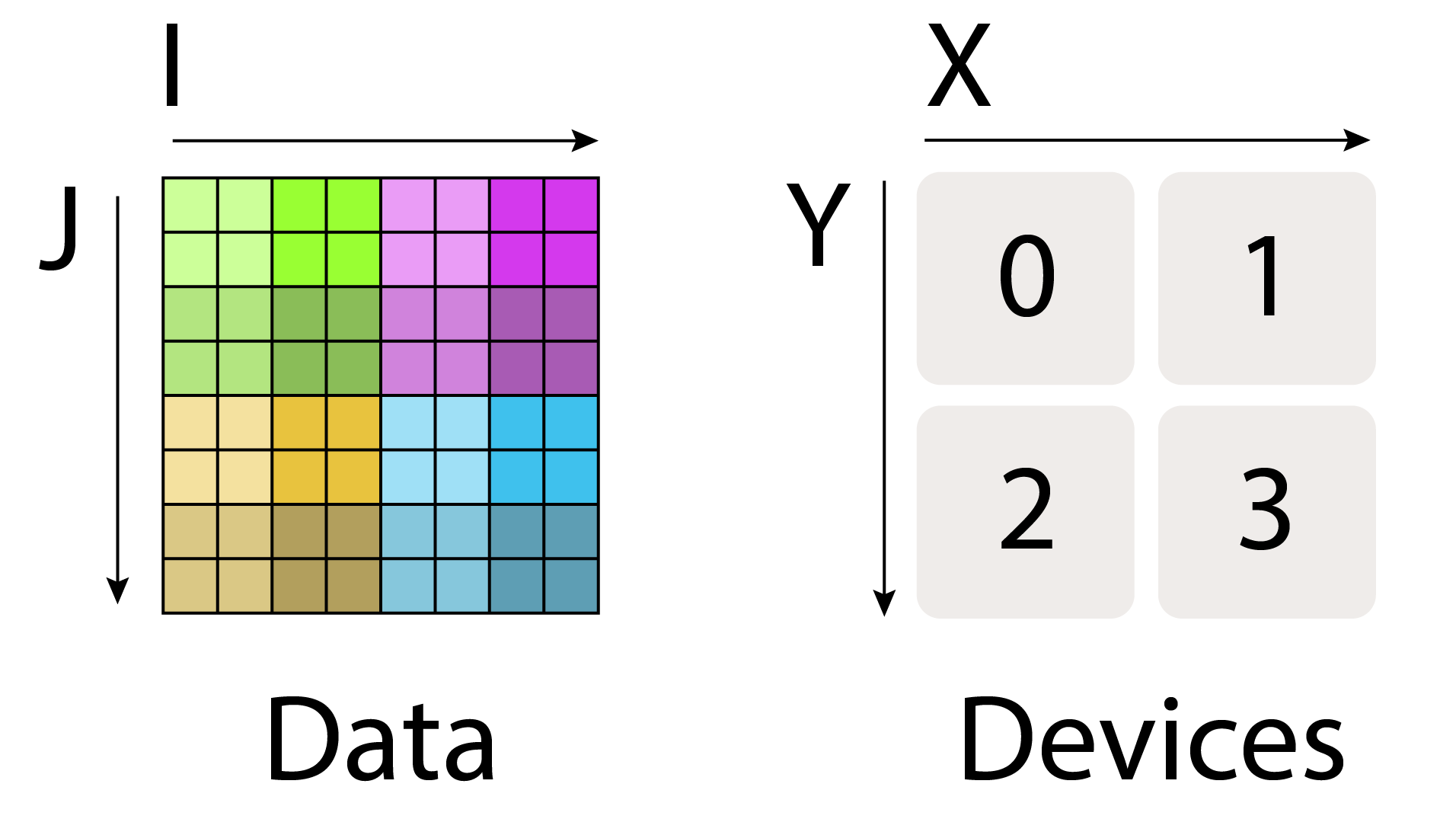
我们将矩阵的完全复制形式简单地写为 $A[I, J]$，没有任何分片分配。这意味着每个设备都包含整个矩阵的完整副本。

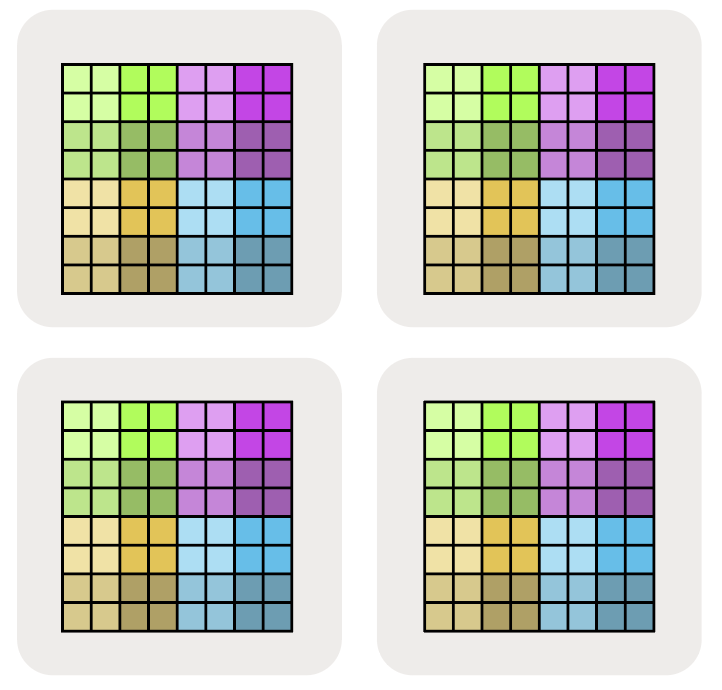
我们可以用一个下标网格轴来表示其中一个维度已经跨一个网格轴进行了分区。例如 $A[I_X, J]$ 意味着 I 逻辑轴已经跨 X 网格维度进行了分区，但是 J 维度没有被分区，并且这些块在 Y 网格轴上保持部分复制。

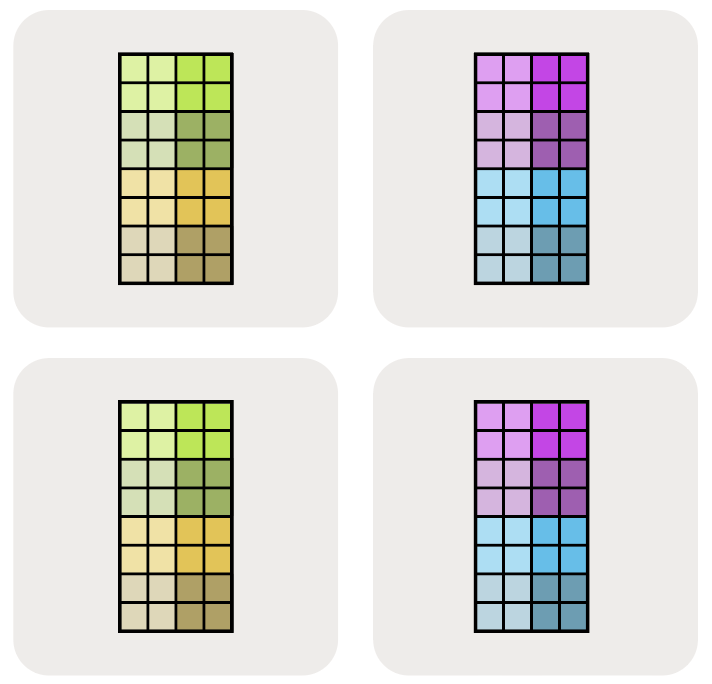
$A[I_X, J_Y]$ 意味着 I 逻辑轴已经跨 X 网格轴进行了分区，并且 J 维度已经跨 Y 网格轴进行了分区。

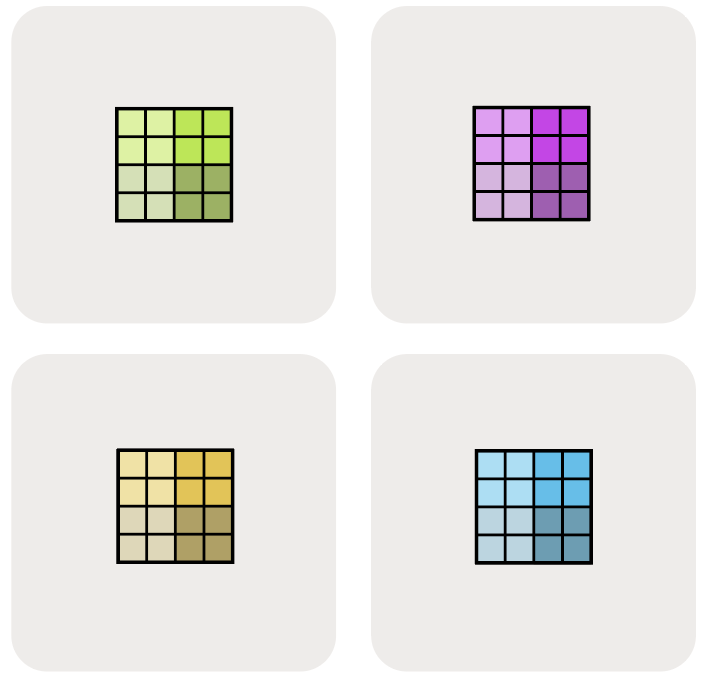
我们在下图中说明了其他可能性：

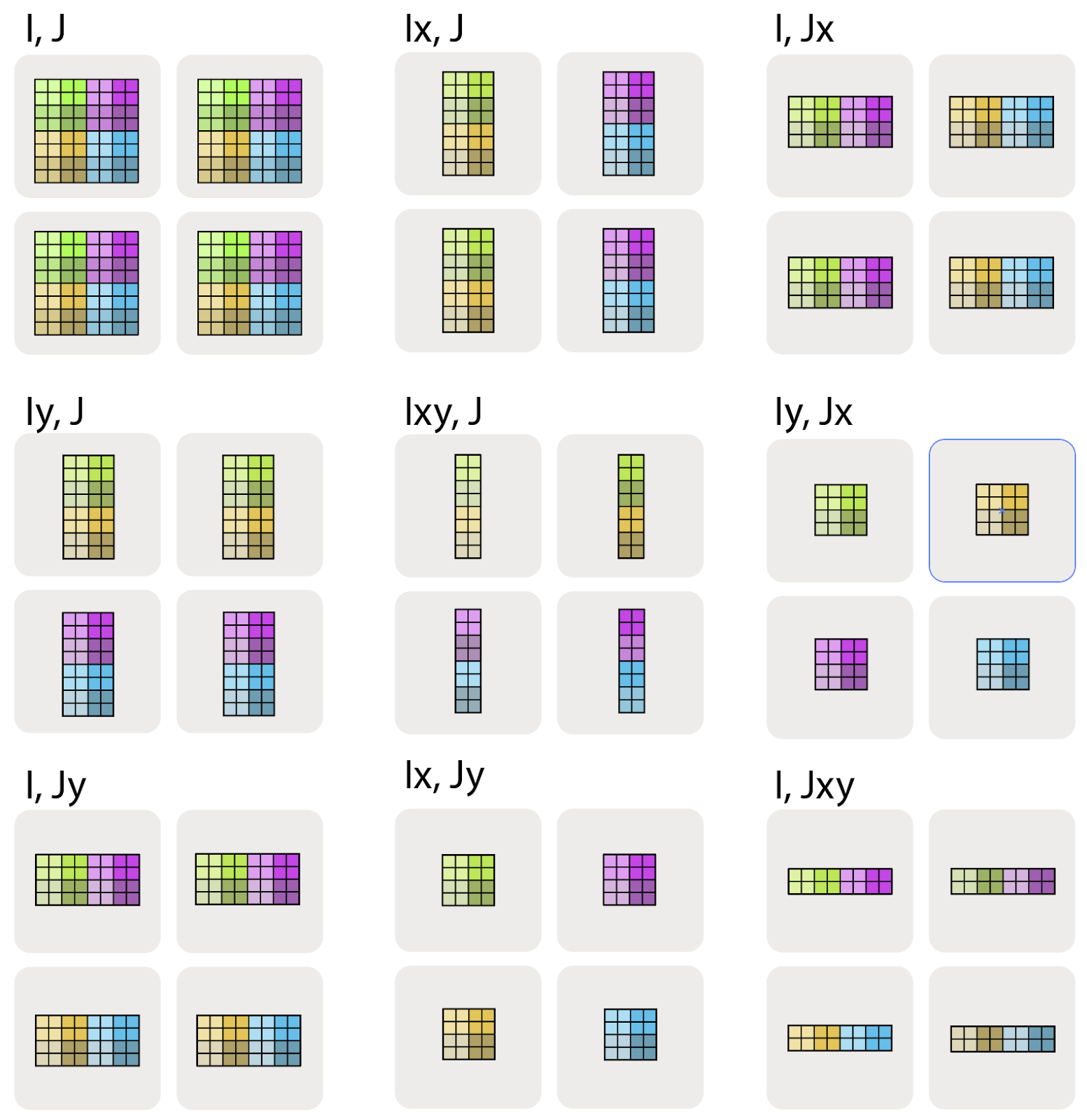
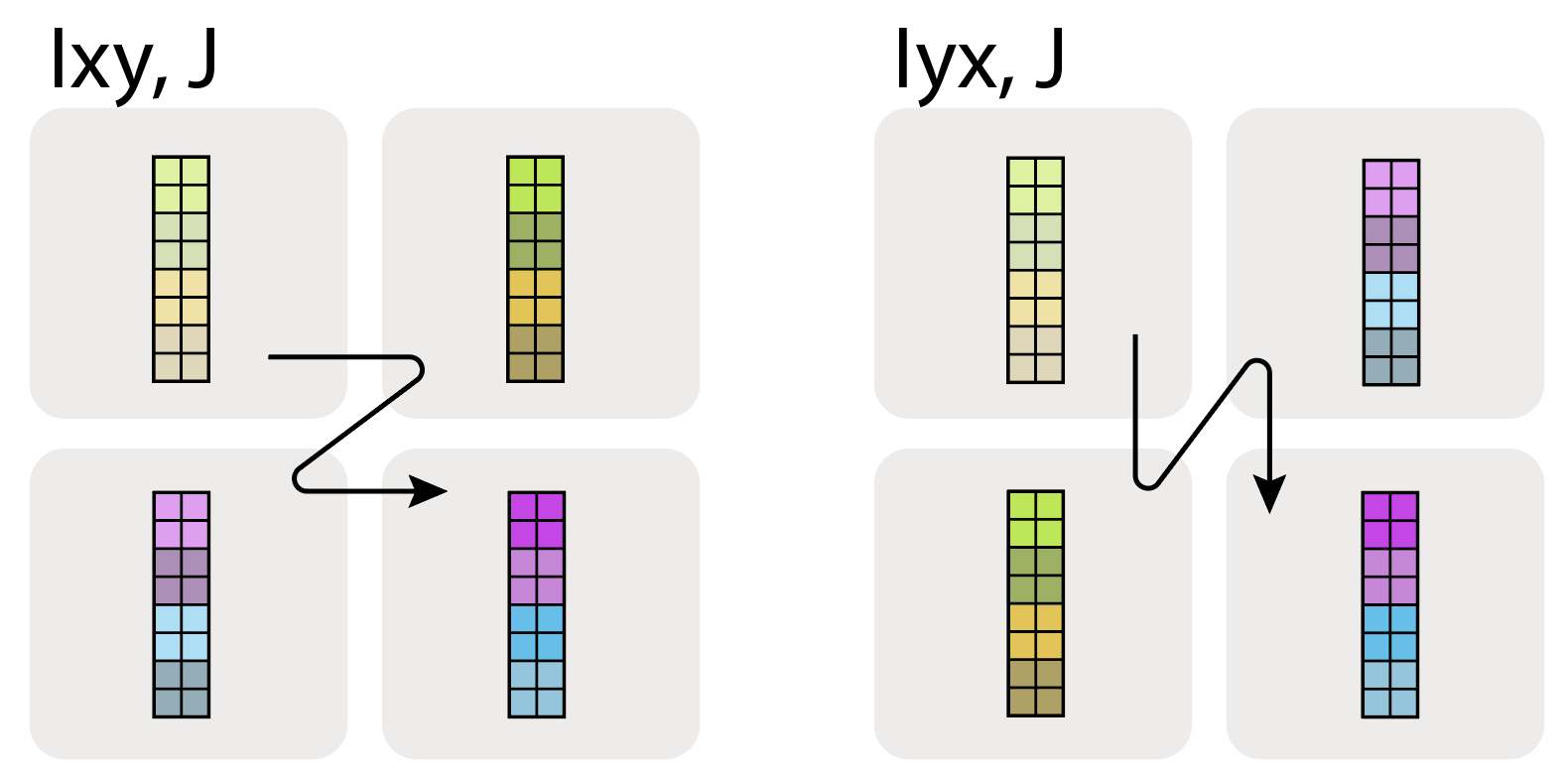
这里 $A[I_{XY}, J]$ 意味着我们将 X 和 Y 网格轴视为一个更大的扁平化维度，并将 I 命名轴跨所有设备进行分区。多个网格轴下标的顺序很重要，因为它指定了跨网格分区的遍历顺序。

最后，请注意我们不能将多个命名轴沿同一个网格维度进行分片。例如，$A[I_X, J_X]$ 是一个无意义的、被禁止的分片方式。一旦一个网格维度被用于分片数组的一个维度，它在某种意义上就被“用掉”了。

小测验： 设 A 是一个形状为 int8[128, 2048] 的数组，分片方式为 $A[I_{XY}, J]$，设备网格为 Mesh({'X': 2, ‘Y': 8, ‘Z': 2})（总共 32 个设备）。A 在每个设备上使用多少内存？A 在所有设备上总共使用多少内存？

点击此处查看答案。

答案： 我们的数组 A 在 X 和 Y 上分片，在 Z 上复制，所以每个设备的形状是 int8[128 / (2 * 8), 2048] = int8[8, 2048]，大小为 8 * 2048 = 16,384 字节。因为它在 Z 上复制，而在一个 Z 平面内它在 X 和 Y 上完全分片，所以每个 Z 平面都有一份它的副本，并且有 2 个这样的平面，所以总大小（在所有设备上）是 128 * 2048 * 2 = 512 KiB。

我们如何在代码中描述它？

到目前为止，我们一直避免谈论代码，但现在是预览的好机会。JAX 使用一种与我们上面描述的抽象语法非常匹配的命名分片语法。我们将在第 10 节中更多地讨论这一点，但这里有一个快速预览。你可以在 Google Colab 这里尝试，并分析结果以查看 JAX 如何处理不同的分片方式。这个代码片段做了 3 件事：

创建一个 jax.Mesh，将我们的 8 个 TPU 映射到一个 4x2 的网格中，并将名称 ‘X’ 和 ‘Y’ 分配给两个轴。
创建矩阵 A 和 B，其中 A 在其两个维度上都进行了分片，而 B 在输出维度上进行了分片。
编译并执行一个简单的矩阵乘法，返回一个分片数组。

import jax
import jax.numpy as jnp

# 创建我们的网格！我们在一个 TPU v2-8 4x2 切片上运行，名称为 'X' 和 'Y'。
assert len(jax.devices()) == 8
mesh = jax.make_mesh(axis_shapes=(4, 2), axis_names=('X', 'Y'))

# 一个小工具函数来帮助定义我们的分片。PartitionSpec 是我们的
# 分片（从轴到名称的映射）。
def P(*args):
  return jax.NamedSharding(mesh, jax.sharding.PartitionSpec(*args))

# 我们在非收缩维度上对 A 和 B 进行分片，并在收缩维度上对 A 进行分片。
A = jnp.zeros((8, 2048), dtype=jnp.bfloat16, device=P('X', 'Y'))
B = jnp.zeros((2048, 8192), dtype=jnp.bfloat16, device=P(None, 'Y'))

# 我们可以对这些分片数组执行矩阵乘法！out_shardings 告诉我们我们希望
# 输出如何分片。JAX/XLA 为我们处理其余的分片工作。
y = jax.jit(lambda A, B: jnp.einsum('BD,DF->BF', A, B), out_shardings=P('X', 'Y'))(A, B)

关于 JAX 的酷炫之处在于，这些数组的行为就像它们没有被分片一样！B.shape 会告诉我们全局或逻辑形状 (2048, 8192)。我们必须实际查看 B.addressable_shards 才能看到它是如何进行本地分片的。我们可以对这些数组执行操作，JAX 会尝试找出如何广播或重塑它们以执行这些操作。例如，在上面的例子中，A 的本地形状是 [2, 1024]，B 的本地形状是 [2048, 4096]。JAX/XLA 会自动在这些数组之间添加必要的通信以执行最终的乘法。

分片数组的计算

如果你有一个分布在多个设备上的数据数组，并希望对其执行数学运算，那么与分片数据和计算相关的开销是什么？

显然，这取决于所涉及的计算。

对于逐元素操作，对分布式数组进行操作没有开销。
当我们希望对驻留在多个设备上的元素执行操作时，事情就变得复杂了。幸运的是，对于大多数机器学习，几乎所有的计算都以矩阵乘法的形式进行，而且它们相对容易分析。

本节的其余部分将讨论如何乘法分片矩阵。粗略地说，这涉及到移动矩阵的块，以便你可以完全乘法或求和每个块。每种分片方式都将涉及不同的通信。例如，$A[I_X, J] \cdot B[J, K_Y] \to C[I_X, K_Y]$ 可以在没有任何通信的情况下进行乘法，因为收缩维度（J，我们实际求和的维度）是未分片的。然而，如果我们希望输出是未分片的（即 $A[I_X, J] \cdot B[J, K_Y] \to C[I, K]$），我们就需要将 $A$ 或 $C$ 复制到每个设备（使用 AllGather）。这两种选择有不同的通信成本，所以我们需要计算这个成本并选择最低的一个。

你可以从“块矩阵乘法”的角度来思考这个问题。

要理解这一点，回顾一下“块矩阵”的概念会很有帮助，它是一个嵌套的矩阵的矩阵：

\begin{matrix} (1) & (\begin{matrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \end{matrix}) = (\begin{matrix} [\begin{matrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{matrix}] \\ [\begin{matrix} a_{20} & a_{21} \\ a_{30} & a_{31} \end{matrix}] \end{matrix} \begin{matrix} [\begin{matrix} a_{02} & a_{03} \\ a_{12} & a_{13} \end{matrix}] \\ [\begin{matrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{matrix}] \end{matrix}) = (\begin{matrix} A_{00} & A_{01} \\ A_{10} & A_{11} \end{matrix}) \end{matrix}

矩阵乘法有一个很好的性质，即当矩阵乘数用块来表示时，乘积可以用块矩阵乘法来表示，遵循标准规则：

\begin{matrix} (2) & (\begin{matrix} A_{00} & A_{01} \\ A_{10} & A_{11} \end{matrix}) \cdot (\begin{matrix} B_{00} & B_{01} \\ B_{10} & B_{11} \end{matrix}) = (\begin{matrix} A_{00} B_{00} + A_{01} B_{10} & A_{00} B_{01} + A_{01} B_{11} \\ A_{10} B_{00} + A_{11} B_{10} & A_{10} B_{01} + A_{11} B_{11} \end{matrix}) \end{matrix}

这意味着实现分布式矩阵乘法可以归结为在网络上传输这些分片块，对这些块执行本地矩阵乘法，并对它们的结果求和。问题就在于添加什么通信，以及它的成本有多高。

方便的是，我们可以将所有可能的分片情况归结为我们需要考虑的大约 4 种情况，每种情况都有一条规则来说明我们需要添加什么通信。

情况 1： 两个输入都没有在收缩维度上进行分片。我们可以 без任何通信地乘法本地分片。
情况 2： 一个输入有分片的收缩维度。我们通常对分片的输入沿收缩维度进行“AllGather”。
情况 3： 两个输入都在收缩维度上进行了分片。我们可以乘法本地分片，然后对结果进行“AllReduce”。
情况 4： 两个输入都有一个非收缩维度沿相同轴分片。我们必须先对其中一个输入进行 AllGather 才能继续。

你可以把这些看作是需要遵守的规则，但理解这些规则为什么成立以及它们的成本有多高也很有价值。我们现在将详细讨论每一种情况。

情况 1：两个乘数都没有分片的收缩维度

引理： 当乘法分片矩阵时，计算是有效的，并且输出遵循输入的分片方式，除非收缩维度被分片或者两个矩阵都沿同一个轴分片。例如，这样可以正常工作

A [I_{X}, J] \cdot B [J, K_{Y}] \to C [I_{X}, K_{Y}]

完全不需要任何通信，并产生一个跨 X 和 Y 硬件维度分片的张量。试着思考一下为什么会这样。基本上，计算与分片无关，因为每个批次条目都有一些本地的收缩轴块，它可以进行乘法和规约。以下任何一种情况都可以正常工作并遵循此规则：

\begin{aligned} A [I, J] \cdot B [J, K] \to & C [I, K] \\ A [I_{X}, J] \cdot B [J, K] \to & C [I_{X}, K] \\ A [I, J] \cdot B [J, K_{Y}] \to & C [I, K_{Y}] \\ A [I_{X}, J] \cdot B [J, K_{Y}] \to & C [I_{X}, K_{Y}] \end{aligned}

因为 A 和 B 都没有分片的收缩维度 J，我们可以简单地执行输入的本地块矩阵乘法，结果将已经按照期望的输出分片方式进行了分片。当两个乘数都有沿相同轴分片的非收缩维度时，情况就不再是这样了（详见无效分片部分）。

情况 2：一个乘数有分片的收缩维度

让我们考虑当一个输入 A 沿收缩维度 J 分片，而 B 完全复制时该怎么做：

A [I, J_{X}] \cdot B [J, K] \to C [I, K]

我们不能简单地乘法 A 和 B 的本地块，因为我们需要对 A 的整个收缩维度求和，而这个维度是跨 X 轴分割的。通常，我们首先对 A 的分片进行“AllGather”，这样每个设备都有一个完整的副本，然后才与 B 相乘：

{AllGather}_{X} [I, J_{X}] \to A [I, J]

A [I, J] \cdot B [J, K] \to C [I, K]

这样，实际的乘法就可以在每个设备上完全完成。

要点： 当乘法矩阵时，如果其中一个矩阵沿收缩维度分片，我们通常先对其进行 AllGather，这样收缩就不再是分片的，然后再进行本地矩阵乘法。

注意，当 B 没有同时沿 X 轴分片时，我们也可以进行本地部分矩阵乘法，然后对分片的部分和进行求和（或 AllReduce），这在某些情况下可能更快。参见下面的问题 4。

什么是 AllGather？ AllGather 是我们将要讨论的第一个核心 MPI 通信原语。AllGather 移除沿一个轴的分片，并将分布在设备上的分片重新组装到该轴上的每个设备上。使用上面的表示法，AllGather 从一组轴中移除一个下标，例如

{AllGather}_{X Y} (A [I_{X Y}, J]) \to A [I, J]

我们不必移除给定维度的所有下标，例如 $A [I_{X Y}, J] \to A [I_{Y}, J]$ 也是一个 AllGather，只是仅在一个轴上进行。另外请注意，我们可能也希望使用 AllGather 来移除非收缩维度的分片，例如在矩阵乘法中：

A [I_{X}, J] \cdot B [J, K] \to C [I, K]

我们可以先对 A 进行 AllGather 以移除输入分片，或者我们可以进行分片矩阵乘法，然后对结果 C 进行 AllGather。

AllGather 是如何实际执行的？ 为了在一个 TPU 轴（一个环）周围执行一维 AllGather，我们基本上让每个 TPU 将其分片在一个环上传递，直到每个设备都有一个副本。GPU AllGather 也可以这样工作，你可以在一个节点中的 GPU 之间创建一个环，并按那个（任意）顺序传递数据块。这是一个动画：

图：一个动画，展示了如何在一组 8 个 TPU 或 GPU 设备上执行 AllGather。每个设备开始时拥有数组的 1/8，最终得到一个完整的副本。

我们可以单向或双向进行 AllGather（上图显示的是双向）。如果我们单向进行，每个 TPU 在环上发送大小为 $\text{bytes} / N$ 的数据块，共 $N - 1$ 跳。如果我们双向进行，我们有 $\lceil \frac{N}{2} \rceil$ 跳，每跳大小为 $2 \cdot \text{bytes} / N$。

这需要多长时间？ 让我们以双向 AllGather 为例，计算它需要多长时间。设 $V$ 为数组的字节数，X 为收缩维度上的分片数。那么从上图中，每跳在每个方向发送 $V / |X|$ 字节，所以每跳需要

T_{h o p} = \frac{2 \cdot V}{X \cdot W_{ici}}

其中 $W_\text{ici}$ 是双向 ICI 带宽。分子中的因子 2 来自于我们使用的是双向带宽。我们在每个方向发送 $V / X$，总共是 $2V / X$。我们需要发送总共 $|X| / 2$ 跳才能到达每个 TPU技术上是 $\lceil X / 2 \rceil$，所以总的规约需要

T_{t o t a l} = \frac{2 \cdot V \cdot X}{2 \cdot X \cdot W_{ici}}

T_{t o t a l} = \frac{V}{W_{ici}}

注意，这不依赖于 $X$！ 这有点令人惊讶，因为它意味着即使我们的 TPU 只是局部连接的，连接的局部性也不重要。我们只是受限于每个链接的速度。

要点： 当在吞吐量受限的情况下执行 AllGather（或 ReduceScatter 或 AllReduce）时，实际的通信时间仅取决于数组的大小和可用带宽，而不取决于数组分片的设备数量！

关于 ICI 延迟的说明： 每次通过 ICI 链路的跳跃都有一些固有的开销，无论数据量大小。这通常在 1us 左右。这意味着当我们的数组 $A$ 非常小，每跳时间小于 1us 时，我们可能会进入一个“延迟受限”的状态，此时计算确实依赖于 $X$。

点击此处查看完整细节。

设 $T_{min}$ 为单次跳跃的最小时间。那么

T_{h o p} = max [T_{m i n}, \frac{2 \cdot V}{X \cdot W_{ici}}]

T_{t o t a l} = max [\frac{T_{m i n} \cdot X}{2}, \frac{V}{W_{ici}}]

因为我们执行了 $X / 2$ 次跳跃。对于大型的规约或收集操作，我们是完全受带宽限制的。我们发送的数据量如此之大，以至于每次跳跃的开销基本上可以忽略不计。但对于小型数组（例如，从模型中采样时），这个开销是不可忽略的，ICI 带宽也无关紧要。我们纯粹受延迟限制。换句话说，对于特定的 TPU，例如 TPU v5e，其单向 ICI 带宽为 4.5e10，发送任何小于 4.5e10 * 1e-6 = 45kB 的缓冲区都将是延迟受限的。

这是一个在 TPU v5e 8x16 切片上 AllGather 带宽的实证测量。数组跨 16 个轴进行分片，因此它有一个完整的双向环。

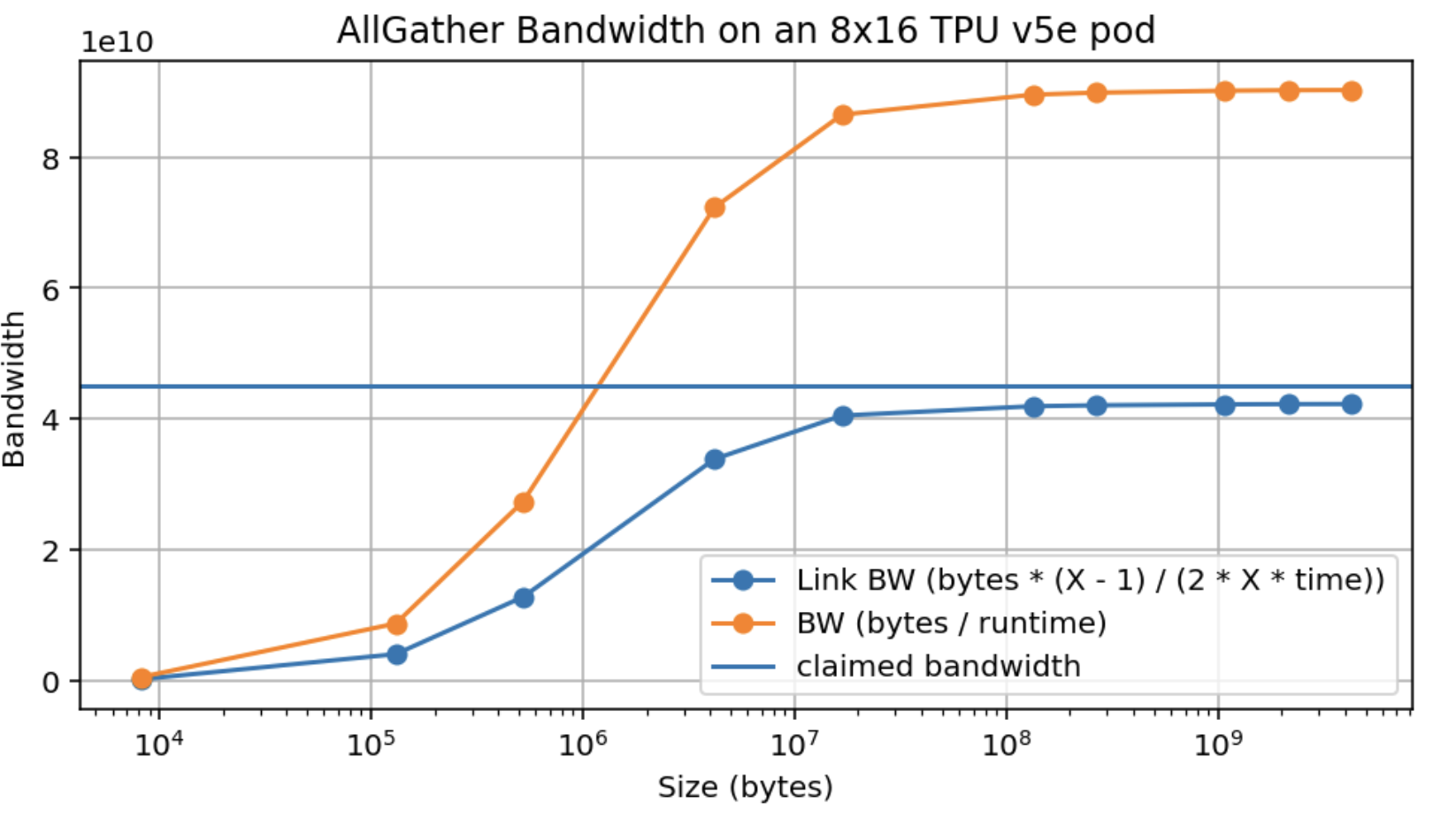
图：TPU v5e 在 AllGather 期间的实证带宽和估计链路带宽。橙色曲线是每秒实际 AllGather 的字节数，而蓝色曲线显示了根据集合操作已知成本计算出的实证单向链路带宽。

请注意，我们只达到了声称的峰值带宽（4.5e10）的约 95%，并且我们在大约 10MB 时达到这个峰值，当进行 16 路分片时，每个设备约 500kB（*旁注：这比 GPU 好得多）。

当我们跨多个轴进行 AllGather 时会发生什么？ 当我们跨多个轴进行收集时，我们有多个维度的 ICI 来执行收集。例如，AllGather_XY([B, D_XY]) 在两个硬件网格轴上操作。这将可用带宽增加了 $N_\text{axes}$ 倍。

点击此处查看完整细节。

通常我们有

T_{t o t a l} = max [\frac{T_{m i n} \cdot \sum_{i} | X_{i} |}{2}, \frac{V}{W_{ici} \cdot N_{axes}}]

其中 $\sum_{i} | X_{i} | / 2$ 是 TPU 网格中最长路径的长度。

小测验 2 [AllGather 时间]： 使用第 2 部分中的数据，在 TPUv5e 上使用 2D 网格 {'X': 8, 'Y': 4}， $E = 2048$ ， $F = 8192$ ，以 bfloat16 格式执行 AllGather_Y([E_Y, F]) → [E, F] 需要多长时间？如果 $E = 256, F = 256$ 呢？

点击此处查看答案。

答案： 让我们先计算一些基本量：

1) TPU v5e 在其 2 个轴上各有 4.5e10 字节/秒的单向 ICI 带宽。 2) 对于 (a) 中的 bfloat16，我们有 $A[E_Y, F]$，所以每个设备持有一个形状为 bfloat16[512, 8192] 的数组，其大小为 512 * 8192 * 2 = 8.4MB。总数组大小为 2048 * 8192 * 2 = 34MB。

对于第 (1) 部分，我们可以使用上面的公式。由于我们是在一个轴上执行 AllGather，我们有 $T_{\text{comms}} = \text{34e6} / \text{9e10} = \text{377us}$。为了检查我们是否受延迟限制，我们知道在一个大小为 4 的轴上，最多有 3 次跳跃，所以我们的延迟限制大约是 3us，所以我们离得不近。然而，TPU v5e 只有一个轴大小为 16 时才有环回连接，所以这里我们实际上无法进行完全双向的 AllGather。我们需要 3 次跳跃才能让数据从边缘到达另一边，所以理论上我们有更像 $T_{\text{comms}} = 3 * \text{8.4e6} / \text{4.5e10} = 560\mu s$。这是来自这个 Colab 的实际性能分析，显示为 $680 \mu s$，这是合理的，因为我们可能没有达到 100% 的理论带宽！对于第 (2) 部分，每个分片的大小是 64 * 256 * 2 = 32kB。32e3 / 4.5e10 = 0.7us，所以我们是延迟受限的。由于我们有 3 次跳跃，这将花费大约 3 * 1us = 3us。实际上，它更接近 8us。

情况 3：两个乘数都有分片的收缩维度

第三种基本情况是当两个乘数都在它们的收缩维度上分片，且沿同一个网格轴：

A [I, J_{X}] \cdot B [J_{X}, K] \to C [I, K]

在这种情况下，本地分片块矩阵乘法至少是可能执行的，因为它们将共享相同的收缩索引集。但是每个乘积只代表最终期望乘积的部分和，并且沿 X 维度的每个设备将剩下这个最终期望乘积的不同部分和。这种情况非常普遍，以至于我们扩展了我们的表示法来明确标记这种情况：

A [I, J_{X}] \cdot_{LOCAL} B [J_{X}, K] \to C [I, K] {U_{X}}

符号 { U_X } 读作“沿 X 网格轴未规约”，指的是操作在某种意义上是“未完成”的状态，因为它只有在最终求和后才算完成。$\cdot_\text{LOCAL}$ 语法意味着我们执行本地求和，但将结果保持未规约状态。

这可以看作是关于矩阵乘法和外积的以下结果：

A \cdot B = \sum_{i = 1}^{P} \underset{\in R^{n \times m}}{\underset{⏟}{A_{:, i} \otimes B_{i, :}}}

其中 ⊗ 是外积。因此，如果 X 轴上的 TPU i 拥有 A 的第 i 列和 B 的第 i 行，我们可以进行本地矩阵乘法得到 $A_{:, i} \otimes B_{i, :} \in R_{n \times m}$ 。这个矩阵的每个条目都包含 A • B 在该条目处的和的第 i 项。我们仍然需要对 P 进行求和，我们将其沿网格轴 X 进行了分片，以获得完整的 A • B。如果我们用块（即分片）来写 A 和 B，然后对结果的每个分片求和，其工作方式是相同的。

我们可以使用一个完整的 AllReduce 跨 X 轴来执行这个求和来解决这个问题：

\begin{aligned} A [I, J_{X}] \cdot_{LOCAL} B [J_{X}, K] \to & C [I, K] {U_{X}} \\ {AllReduce}_{X} C [I, K] {U_{X}} \to & C [I, K] \end{aligned}

AllReduce 移除部分和，导致沿该轴的每个设备都具有相同的完全求和的值。AllReduce 是我们本节将讨论的几个关键通信中的第二个，第一个是 AllGather，其他的是 ReduceScatter 和 AllToAll。AllReduce 接受一个具有未规约（部分求和）轴的数组，通过在未规约轴上传递这些分片并累加结果来执行求和。其签名为

{AllReduce}_{Y} A [I_{X}, J] {U_{Y}} \to A [I_{X}, J]

这意味着它只是移除了 ${U_Y}$ 后缀，但其他方面保持结果不变。

AllReduce 的成本有多高？ 一个关于 AllReduce 如何执行的心智模型是，每个设备将其分片发送给其邻居，并对收到的所有分片进行求和。显然，这比 AllGather 更昂贵，因为每个“分片”都与完整数组具有相同的形状。通常，一个 AllReduce 的成本是 AllGather 的两倍。 一种理解方式是注意到 AllReduce 可以表示为另外两个原语的组合：一个 ReduceScatter 和一个 AllGather。与 AllReduce 一样，ReduceScatter 解决数组上的部分和，但结果是沿给定维度“散布”或分区的输出。AllGather 收集所有这些片段，并“取消分区/取消分片/复制”该物理轴上的逻辑轴。

\begin{aligned} {ReduceScatter}_{Y, J} : A [I_{X}, J] {U_{Y}} \to & A [I_{X}, J_{Y}] \\ {AllGather}_{Y} : A [I_{X}, J_{Y}] \to & A [I_{X}, J] \end{aligned}

那么 ReduceScatter 呢？ 正如 AllReduce 移除一个下标（上面 $F_Y \to F$），ReduceScatter 对一个未规约/部分求和的数组求和，然后将另一个逻辑轴沿同一个网格轴散布（分片）。$[F]\{U_Y\} \to [F_Y]$。动画展示了这是如何完成的：注意它与 AllGather 非常相似，但我们不是保留每个分片，而是将它们加在一起。因此，它的延迟大致相同，不包括执行规约所需的时间。

每跳的通信时间就是每个分片的字节数 $V / Y$ 除以带宽 $W_\text{ici}$，就像 AllGather 一样，所以我们有

T_{comms per AllGather or ReduceScatter} = \frac{V}{W_{ici}}

T_{comms per AllReduce} = 2 \cdot \frac{V}{W_{ici}}

其中 $W_{ici}$ 是双向带宽，只要我们有一个完整的环来进行规约。

情况 4：两个乘数都有一个非收缩维度沿相同轴分片

在对张量进行分片时，每个网格维度最多只能出现一次。执行上述规则有时会导致违反此规则的情况，例如：

A [I_{X}, J] \cdot B [J, K_{X}] \to C [I_{X}, K_{X}]

这是无效的，因为沿维度 X 的一个给定分片，比如说 i，将拥有 C 的第 (i, i) 个分片，即一个对角线条目。那么，在所有分片中没有足够的信息来恢复除结果的对角线条目之外的任何东西，所以我们不能允许这种分片。

解决这个问题的方法是对某些维度进行 AllGather。这里我们有两个选择：

\begin{aligned} {AllGather}_{X} A [I_{X}, J] \to & A [I, J] \\ A [I, J] \cdot B [J, K_{X}] \to & C [I, K_{X}] \end{aligned}

或

\begin{aligned} {AllGather}_{X} B [J, K_{X}] \to & B [J, K] \\ A [I_{X}, J] \cdot B [J, K] \to & C [I_{X}, K] \end{aligned}

在任何一种情况下，结果的形状中只会提到 X 一次。我们选择哪一个将取决于后续操作需要什么样的分片。

深入了解 TPU 通信原语

前面的 4 种情况介绍了用于执行分片矩阵乘法的几个“核心通信原语”：

AllGather： 从分片中移除一个下标，收集分片。
ReduceScatter： 通过对该轴上的分片求和，从数组中移除一个“未规约”后缀，使数组在第二个轴上保持分片。
AllReduce： 移除一个“未规约”后缀，使数组在该轴上保持未分片。

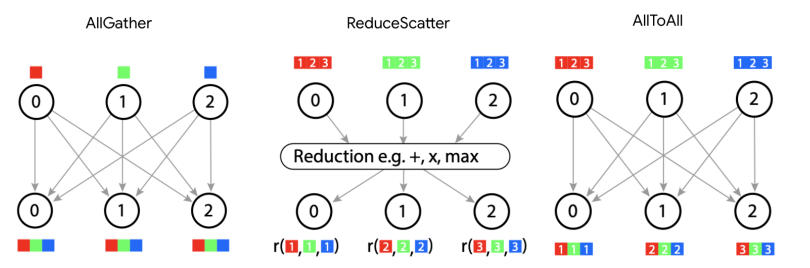
还有最后一个核心通信原语需要提及，它出现在专家混合（MoE）模型和其他计算中：AllToAll。

我们最后的通信原语：AllToAll

最后一个基本集合操作，在考虑分片矩阵乘法时不会自然出现，但在实践中经常出现，是 AllToAll 集合操作，或者更准确地说是分片转置或重分片操作的特例。例如

{AllToAll}_{X, J} A [I_{X}, J] \to A [I, J_{X}]

AllToAll 通常用于在分片计算的不同区域之间重新排列分片布局，这些区域没有兼容的布局方案。在考虑分片专家混合模型时，它们会自然出现。你可以把 AllToAll 看作是将一个下标从一个轴移动到另一个轴。因为 AllToAll 不需要将每个分片的所有数据复制到环上的所有设备，所以它实际上比 AllGather 更便宜（便宜 1/4）对于偶数大小的双向环，每个设备将向右发送 $(N/2 + (N/2-1) + \ldots + 1)$ 个块，向左发送 $((N/2-1) + \ldots + 1)$ 个块 $= 0.5 \cdot (N / 2) \cdot (N/2 + 1) + 0.5 \cdot (N / 2) \cdot (N/2 - 1) = N^2/4$。每个块（即分片的分片）的大小是 $\text{bytes} / N^2$，所以每个设备的成本是 $(\text{bytes} / N^2) \cdot N^2 / 4 = \text{bytes} / 4$。这个结果在所有设备上都是可扩展的，因为总带宽随设备数量而扩展。。

如果我们推广到 ND AllToAll，在 AxBxC 网格上一个大小为 $V$ 字节的数组的总成本是

T_{comms per AllToAll} = \frac{V \cdot max (A, B, C, . . .)}{4 \cdot N \cdot W_{ici}}

其中 $W_\text{ici}$ 照例是双向 ICI 带宽。对于 1D 网格，这简化为 $V / (4 \cdot W_\text{ici})$，这是 AllReduce 成本的 1/4。在 2D 中，成本实际上随着最小轴的大小而降低。

旁注：如果你想要一个粗略的推导，从一个 1D 环 $\mathbb{Z} / N\mathbb{Z}$ 开始。如果我们随机选择一个源节点和一个目标节点，它们平均相距 N / 4 跳，这给了我们一个 $(V \cdot N) / (4 * N)$ 的成本。现在如果我们考虑一个 ND 环，每个轴基本上是独立的。每个节点有 $1 / Z$ 字节，平均需要将其数据跳跃 $\max(A, B, C, \ldots) / 4$ 跳。

关于 ReduceScatter 的更多信息

ReduceScatter 是一个比它初看起来更基本的操作，因为它实际上是 AllGather 的导数，反之亦然。也就是说，如果在前向传播中我们有：

{AllGather}_{X} A [I_{X}] \to A [I]

那么我们对反向模式导数 A’（通常在每个分片上都不同）进行 ReduceScatter，以推导出分片的 A’：

{ReduceScatter}_{X} A^{'} [I] {U_{X}} \to A^{'} [I_{X}]

同样地，前向传播中的 ${ReduceScatter}_{X} (A [I] {U_{X}}) \to A [I_{X}]$ 意味着后向传播中的 ${AllGather}_{X} (A^{'} [I_{X}]) \to A^{'} [I]$ 。

将 AllReduce 转换为 AllGather 和 ReduceScatter 还有一个方便的特性，即我们可以将最终的 AllGather 推迟到稍后的某个时刻。我们通常不想支付重新组装跨设备复制的完整矩阵乘积的成本。相反，我们希望即使在组合两个具有分片收缩维度的乘数的情况下，也能保持分片状态：

A [I, J_{X}] \cdot B [J_{X}, K] \to C [I, K_{X}]

在这种情况下，我们也可以执行 ReduceScatter 而不是 AllReduce，然后可以选择在稍后的某个时间执行 AllGather，即

\begin{aligned} A [I, J_{X}] \cdot_{L O C A L} B [J_{X}, K] \to & C [I, K] {U_{X}} \\ {ReduceScatter}_{X, K} C [I, K] {U_{X}} \to & C [I, K_{X}] \end{aligned}

请注意，ReduceScatter 引入了一个分片维度，因此在这种情况下，它自然可以自由地沿 I 或 K 命名维度进行分片。在使用 ReduceScatter 时，我们通常需要选择哪个命名维度来引入新的分片（尽管选择通常由更大的建模上下文强制决定）。这就是为什么我们使用 ReduceScatter_X,K 语法来指定要分片的轴。

我们学到了什么？

数组的分片由一个网格（Mesh）和一个分片（Sharding）指定。网格为我们 TPU 网格的物理硬件轴命名，分片将网格轴名称分配给数组的逻辑轴。
- 例如，A[I_XY, J] 描述了一个抽象数组 A，其第一个维度沿两个网格轴 X 和 Y 进行分片。结合 Mesh(mesh_shape=(4, 8), axis_names=(‘X’, ‘Y’)) 或简写的 Mesh({‘X’: 4, ‘Y’: 8})，这告诉我们我们的数组沿第一个维度进行了 32 路分片。
分片数组的算术运算与未分片数组完全一样，除非你在分片轴上执行收缩操作。在这种情况下，我们必须引入一些通信。我们考虑四种情况：
1. 两个数组都没有在收缩维度上分片：不需要通信。
2. 一个数组在收缩维度上分片（或者收缩维度沿不同轴分片）：我们在执行操作前对其中一个输入进行 AllGather。
3. 两个数组在收缩维度上完全相同地分片： 我们在本地乘法分片，然后执行 AllReduce 或 ReduceScatter。
4. 两个数组在非收缩维度上沿同一个网格轴分片： 我们先对其中一个输入进行 AllGather。
TPU 大致使用 4 个核心通信原语：
1. AllGather: $[A_X, B] \to [A, B]$
2. ReduceScatter: $[A, B] \{U_X\} \to [A, B_X]$
3. AllToAll: $[A, B_X] \to [A_X, B]$
4. AllReduce: $[A_X, B]\{U_Y\} \to [A_X, B]$ (技术上不是一个原语，因为它结合了 ReduceScatter + AllGather)

这些操作的成本和延迟不依赖于轴的大小（只要它们是带宽受限的），而只依赖于输入数组的大小和链路的带宽。对于单向 AllGather/ReduceScatter：

T_{comm per AllGather or ReduceScatter} = \frac{Data volume}{bandwidth} \cdot \frac{Axis - 1}{Axis} ⟶ \frac{Data volume}{bandwidth (bidirectional)}

AllReduce 由一个 ReduceScatter 和一个 AllGather 组成，因此成本是上述的两倍。AllToAll 只需将分片在环上传递一部分，因此成本是 AllGather 的 ¼。这是一个总结：

操作	描述	语法	运行时间
AllGather	收集分片数组沿一个轴的所有分片，移除一个下标。	$[A_X, B] \to [A, B]$	字节数 / (双向 ICI 带宽 * 轴数)
ReduceScatter	对一个部分求和的数组沿一个轴求和，并将其沿另一个轴分片（添加一个下标）。	$[A, B] \{U_X\} \to [A_X, B]$	与 AllGather 相同
AllReduce	对一个部分求和的数组沿一个轴求和。移除一个 { U_x }。结合了 AllGather 和 ReduceScatter。	$[A_X, B]\{U_Y\} \to [A_X, B]$	2 * AllGather
AllToAll	收集（复制）一个轴，并将另一个维度沿同一个轴分片。	$[A, B_X] \to [A_X, B]$	对于双向环，为 AllGather / 4

一些练习题

这里有一些基于本节内容的有启发性的问题。我们暂时不会提供所有答案，但会尽快写出更多答案。

问题 1 [复制分片]：一个数组的分片方式为 $A[I_X, J, K, \ldots]$（即，只在 $X$ 上分片），设备网格为 Mesh({'X': 4, 'Y': 8, 'Z': 2})。$A$ 在所有芯片上占用的总字节数与单个数组副本大小的比率是多少？

点击此处查看答案。

我们的数组只沿 X 轴分片，其大小为 4，因此每个分片的有效大小为 $[I / 4, J, K, \ldots] = \text{sizeof}(A) / 4$。由于我们的数组在 Y 和 Z 轴上是复制的，总大小为 $Y \cdot Z \cdot \text{sizeof}(A)$，所以总大小与单个芯片大小的比率为 $Y \cdot Z \cdot \text{sizeof}(A) / \text{sizeof}(A) = 16$。

问题 2 [AllGather 延迟]：在 TPUv4p 4x4x4 切片上，使用网格 Mesh({'X': 4, 'Y': 4, 'Z': 4})，如果 $B=1024$ 且 $D=4096$，以 bfloat16 格式，执行 $\text{AllGather}_X([B_X, D_Y])$ 需要多长时间？ ${AllGather}_{X Y} ([B_{X}, D_{Y}])$ 呢？ ${AllReduce}_{Z} ([B_{X}, D_{Y}] {U_{Z}})$ 呢？

点击此处查看答案。

我们在所有轴上都有环回链接，因为我们有一个完整的 4x4x4 立方体，所以我们有 9e10 的双向带宽可用。

因为我们只是在一个轴上进行收集，而另一个轴是分片的，所以我们实际上是在 1 个轴上收集 $2BD / Y$ 字节。如果你只考虑 Y 轴上的一个分片，那么沿 X 轴的 AllGather 就像一个未分片的 AllGather，字节数为 1 / Y。 由于我们的 TPU v4p 的 ICI 带宽是 9e10 字节/秒（双向），这将花费 $2BD / (\text{9e10} \cdot Y) = 2 \cdot 1024 \cdot 4096 / (\text{9e10} \cdot 4) = 23 \mu s$。
我们的带宽是之前的两倍，但我们正在 AllGather 整个数组，所以 T = 2BD / (2 * W) = 2*1024*4096 / (2 * 9e10) = 46us。这远未达到 4us 的延迟限制（每跳 1us），所以我们没问题。
AllReduce 的成本是 AllGather 的两倍。每个分片的大小是 $2BD / (X * Y)$，所以成本大约是 $4BD / (X * Y * W)$，或者大约 4 * 1024 * 4096 / (16 * 9e10) = 11.6us。

问题 3 [延迟受限的 AllGather]：假设我们正在执行一个 $\text{AllGather}_X([B_X])$，但 $B$ 非常小（比如 128）。在 TPUv4p 4x4x4 切片上，使用网格 Mesh({'X': 4, 'Y': 4, 'Z': 4})，以 bfloat16 格式，这需要多长时间？提示：你可能受延迟限制。

点击此处查看答案。

我们的 bfloat16 数组总共只使用 256 字节，每个设备只有 64 字节。由于我们在 TPU v4p 上的轴大小为 4，我们有一个环回链接，所以我们可以双向发送数组。使用 4.5e10 的单向带宽，每跳大约需要 64 / 4.5e10 ~ 0，所以我们肯定是延迟受限的。计算跳数，我们只需 2 跳就可以完成整个收集，所以大约 2us 是一个很好的估计。

问题 4 [矩阵乘法策略]：为了执行 $X[B, D] \cdot_D Y[D_X, F] \to Z[B, F]$，在本节中我们告诉你要执行 $\text{AllGather}_X(Y[D_X, F])$ 并乘法完全复制的矩阵（情况 2，策略 1）。相反，你可以像 $X[B, D_X] \cdot_D Y[D_X, F] \to Z[B, F] \{U_X\}$ 那样乘法本地分片（情况 4，策略 2），然后 $\text{AllReduce}_X(Z[B, F] \{ U_X\})$。这两种策略分别执行多少 FLOPs 和通信？哪种更好，为什么？

点击此处查看答案。

让我们从我们的基线（策略 1）开始。正如我们所展示的，AllGather 的成本是 $2DF / W_\text{ici}$。一旦我们有了完全复制的数组，总计算时间是 $2BDF / C$（其中 $C$ 是我们的加速器 FLOPs/s，因为每个 TPU 执行相同的 FLOPs）。所以我们有

T_{total (Strategy 1)} = max (\frac{2 B D F}{C}, \frac{2 D F}{W_{ici}})

相比之下，新策略（策略 2）在 $2BF$ 字节上进行 AllReduce，成本为 $4BF / W_\text{ici}$，但执行的 FLOPs 少 $1 / X$（因为计算是分片的）。这意味着我们执行 $2\cdot B\cdot D\cdot F / X$ FLOPs，并且得到的 AllReduce 在 bfloat16 中通信 $2 \cdot 2 \cdot B \cdot F$ 字节。因此，我们策略 2（没有 AllGather，只有一个后续的 AllReduce）的总时间大约是

T_{total} = max (\frac{2 B D F}{X \cdot C}, \frac{4 B F}{W_{ici}})

问题是：哪个更大？ 当 $D / (X \cdot C) > 2 / W_\text{ici}$，或者当 $D / 2X > C / W_\text{ici} \approx 2550 \rightarrow X < D / (2 * 2550)$ 时，策略 (2) 是计算受限的。我们可能合理地预期 $D \approx 8k$，所以这大致意味着 $X < 2$，这是不可能的——因此我们基本上总是受通信限制于策略 2。对于基线（策略 1），当 $B < C / W_{ici} = 2550$ 时，我们是通信受限的，这通常是但不总是如此。

所以如果 $B < 2550$，我们在两种情况下都是通信受限的，我们有

T_{comms for Strategy 2} < T_{comms for Strategy 1} \Leftrightarrow \frac{4 B F}{W_{ici}} < \frac{2 D F}{W_{ici}}

当 $D > 2B$ 且 $2B < 5100$ 时成立。这通常是成立的，所以如果我们的批次很小，策略 2 有时会更好。当我们的批次很大时（$B > 2550$），我们有

T_{comms for Strategy 2} < T_{math for Strategy 1} \Leftrightarrow \frac{4 B F}{W_{ici}} < \frac{2 B D F}{C}

当 $2 / W_\text{ici} < D / C$，或者当 $D > 2 * 2550 = 5100$ 时成立，这对于大型模型通常是成立的。所以这种替代策略对于大型模型通常更好，除非 $D$ 很小。

我们为什么不总是这样做？ 嗯，在实践中我们有时可能会这样做，但通常很少有一个矩阵乘法的输入的收缩维度沿一个轴分片，而另一个输入没有在该轴上分片。例如，如果我们正在做 FSDP（在第 5 节中解释），我们会将我们的参数在数据维度上分片，但我们的激活也会沿数据维度分片。所以从这个意义上说，这种情况不常出现。

问题 5 [最小延迟]：假设我想在 TPUv5p 4x4x4 上以尽可能低的延迟执行一个矩阵乘法 $A[B, D] \cdot_D B[D, F] \to C[B, F]$。我的输入应该如何分片？总的 FLOPs 和通信时间是多少？

问题 6： 假设我们想在 TPUv5e 4x4 上执行 $A[I_X, J_Y] \cdot_J B[J_Y, K] \to C[I_X, K]$。我们执行什么通信？通信与计算各花费多少时间？

$A[I_X, J] \cdot_J B[J_X, K_Y] \to C[I_X, K_Y]$ 呢？这是训练中最标准的设置，我们结合了数据、张量和零分片。
$A[I_X, J] \cdot_J B[J, K_Y] \to C[I_X, K_Y]$ 呢？这对于推理是标准的，我们进行纯粹的张量并行（+数据）。

问题 7： 一个典型的 Transformer 块有两个矩阵 $B[D, F]$ 和 $C[F, D]$，其中 $F \gg D$。批大小为 B，整个块是 $C \cdot B \cdot x$ ，其中 $x [B, D]$ 。让我们选择 $D = 8192$ 、 $F = 32768$ 和 $B = 128$ ，并假设一切都是 bfloat16。假设我们在一个 TPUv5e 2x2 切片上运行，但假设每个 TPU 只有 300MB 的可用内存。B、C 和输出应该如何分片以保持在内存限制以下，同时最小化总时间？通信和 FLOPs 各花费多少时间？

问题 8 [挑战]：使用上面的简短代码片段作为模板，分配一个分片数组，并使用 pmap 或 shard_map 对 4 个主要通信原语（AllGather、AllReduce、ReduceScatter 和 AllToAll）进行基准测试。你将需要使用 jax.lax.all_gather、jax.lax.psum、jax.lax.psum_scatter 和 jax.lax.all_to_all。你理解这些函数的语义吗？它们需要多长时间？

问题 9 [分片矩阵乘法的另一种策略？]：上面我们声称，当只有一个矩阵乘法的输入沿其收缩维度分片时，我们应该 AllGather 该分片矩阵并在本地执行收缩。你可能想到的另一种策略是执行分片矩阵乘法，然后对结果进行 AllReduce（就像两个输入都沿收缩维度分片一样），即 $A[I, J_X] *_J B[J, K] \to C[I, K]$ 通过以下方式

$C[I, K] \{ U_X \} = A[I, J_X] \cdot B[J_X, K]$
$C[I, K] = \text{AllReduce}(C[I, K] \{ U_X\})$

回答以下问题：

明确写出这个算法，用于矩阵 $A[N, M]$ 和 $B[M, K]$，使用索引来准确显示在哪个设备上执行了什么计算。假设 $A$ 在 ND 个设备上分片为 $A[I, J_X]$，并且你希望你的输出在所有设备上都是复制的。
现在假设你对最终结果不是在每个设备上复制，而是分片（沿 N 或 K 维度）感到满意。上面的算法会如何改变？
仅从上述策略的通信成本来看（在（b）部分，而不是（a）部分），这个通信成本与我们首先 AllGather A 然后进行矩阵乘法的算法的通信成本相比如何？

点击此处查看答案。

首先计算外积，将结果存储在 $O [N, K] : o_{k j} = \sum_{i} a_{k i} b_{i j}$ 中。注意，重复的索引不是被收缩的那个，因为我们正在做外积。这里的和遍历了我们正在使用的特定设备上存储的 i 值集合。所以，例如，如果我们有一个大小为 16 的收缩轴和 4 个设备，那么在设备 0 上，i 的范围是 {0, 1, 2, 3}；在设备 1 上，i 的范围是 {4, 5, 6, 7}；在设备 2 上，i 的范围是 {8, 9, 10, 11}；在设备 3 上，i 的范围是 {12, 13, 14, 15}。然后 AllReduce 存在于每个设备上的 $O[N, K]$ 的部分和，以形成完整的 $O[N, K]$。
我们可以在第 2 步中进行更便宜的 ReduceScatter，而不是 AllReduce，沿任一轴：$[N, K] \{ U_X \} \to [N_X, K]$ 或 $[N, K] \{ U_X \} \to [N, K_X]$。
如上文所述，进行 AllGather 的成本（当我们受吞吐量限制时）与 ReduceScatter 的成本相同；它仅由我们正在处理的完整矩阵的大小决定。所以在 gather-then-matmul 算法中，这与 $NM$ 成比例（因为我们正在 $\text{AllGather}$-ing $A$）；在 matmul-then-reduce-scatter 算法中，这与 NK 成比例（因为我们正在 reduce-scattering $O$）。所以两种算法的通信成本比是 M/K。

问题 10：AllToAll 的乐趣： 在上表中，注意到执行 AllToAll 的时间比执行 AllGather 或 ReduceScatter 的时间低 4 倍（在我们受吞吐量限制的情况下）。在这个问题中，我们将看到这 4 倍的因子从何而来，并看看如果我们只有单向 ICI 链接而不是双向 ICI 链接，这个因子会如何变化。

让我们先从单向情况开始。想象一下我们有 D 个设备在一个环形拓扑中，如果我们正在对一个 N x N 的矩阵 A 进行 AllGather 或 ReduceScatter，该矩阵分片为 $A[I_X, J]$（为简单起见，假设 $D$ 整除 $N$）。描述这两个集合操作中涉及的通信，并计算在整个算法期间通过单个 ICI 链接传输的标量（浮点数或整数）总数。
现在让我们考虑 AllToAll，仍然在单向 ICI 的情况下。在这种情况下，算法与 all-gather 情况有何不同？计算在此算法中通过单个 ICI 链接传输的标量数量。
你应该发现你对（a）和（b）部分的答案之间的比率是一个很好的数字。用简单的术语解释这个因子从何而来。
现在让我们添加双向通信。这对 all-gather 情况下的总时间有何影响？
添加双向通信对 AllToAll 情况下的总时间有何影响？
现在简单地解释一下在双向环中 AllGather 时间和 AllToAll 时间之间的比率。

点击此处查看答案。

(1) 解：过程很简单：在算法的每一步中，每个设备都会向其最近的邻居发送一个单分片“条带”的矩阵（总共有 $\frac{N}{D} \times N$ 个元素）。这发生 $D - 1$ 次，因为每个分片需要被通信到除了它起始的设备之外的所有设备。所以总共有 $\frac{N^{2} (D - 1)}{D}$ 个标量被每个设备传输，即流过一个 ICI 链接。

答案： $N^{2} (1 - \frac{1}{D})$ ，或者当 $D >> 1$ 时简单地是 $N^{2}$ 。

(2) 解：从通信的角度来看，AllToAll 和 AllGather 之间的关键区别在于，在 AllToAll 中，存在于特定设备上的整个分片不需要被通信到每个其他设备。想象一下存储在特定设备（称之为设备 0）上的分片是 $[A, B, C, D]$ （这里 A,B,C,D 是矩阵，我们想象一个有 4 个设备的环来说明）。现在矩阵 $A$ 不需要被通信到任何地方，矩阵 $B$ 需要最终到达设备 1；矩阵 $C$ 最终到达设备 2；矩阵 $D$ 最终到达设备 3。所以在算法的第一步，我们发送 $B$ 、 $C$ 和 $D$ 到设备 1；在下一步，设备 1 发送 $C$ 和 $D$ 到设备 2；在最后一步，设备 2 只发送 $D$ 到设备 3。在这种情况下传输的总参数数是 $(size of A/B/C/D) * (3 + 2 + 1)$ 。A/B/C/D 的大小（现在在一般情况下）是 $\frac{N^{2}}{D^{2}}$ ，并且再次在一般情况下， $(3 + 2 + 1)$ 项变成了 $((D - 1) + (D - 2) + \dots + 1)$ ，或者 $\frac{(D) (D - 1)}{2}$ 。所以通过单个 ICI 链接传输的总字节数是 $\frac{N^{2} (D - 1)}{D \times 2}$ 。

答案： $\frac{N^{2}}{2} (1 - \frac{1}{D})$ ，或者当 $D >> 1$ 时简单地是 $\frac{N^{2}}{2}$ 。

(3) 解：因子就是 $\frac{1}{2}$ ，即在单向环拓扑上，AllToAll 的成本是 all-gather/ReduceScatter 的一半。回顾上面的推导，这最终来自于在 all-gather 情况下，我们每次都传输相同大小的块，共 $(D - 1)$ 次，即我们正在做求和 $tiny block size * (D + D + D + \dots + D)$ ，而在 AllToAll 情况下，我们正在做求和 $tiny block size * (D + D - 1 + D - 2 + \dots + 1)$ 。因此，这个 2 倍的因子基本上来自于 $1 + 2 + \dots + n = n (n + 1) / 2$ 。

(4) 解：任何一个链接需要承载的总标量数现在减少了 2 倍，因为在双向环中，每个“分片条带”可以同时双向发送。

(5) 解：在这种情况下，我们比单向情况赢得了 4 倍。这最容易通过考虑单个分片条带中每个大小为 (N2/D2) 的块的命运来看，比如说源于设备 0 的那个。现在，我们不是（像在单向情况下）将其中一个块发送 D-1 的距离，另一个块发送 D-2 的距离，一直到 1，而是将条带分成向右或向左移动的块，最大移动距离为 ceil(D/2)。所以相应的和现在变成了 $D / 2 + D / 2 - 1 + D / 2 - 2 + \dots = D / 2 \cdot (D / 2 + 1) / 2$ ，或者在大 $D$ 的极限下是 $D^{2} / 8$ 。与单向情况下的 $D^{2} / 2$ 相比，我们看到我们赢得了 4 倍。

(6) 解：在单向环中，我们看到 AllToAll 的时间已经是 all-gather 时间的两倍快；这来自于我们不需要将我们的完整条带发送到每个设备。然后，当我们添加双向性时，我们看到对于 AllToAll 来说是 4 倍的优势，而对于 all-gather 来说只有 2 倍的优势。将这些比率放在一起，我们就得到了我们所寻求的 4 倍因子。

第 3 部分到此结束！关于第 4 部分（Transformer 数学），请点击这里！

脚注

值得注意的是，我们可能也会为了速度而选择并行化。即使我们可以将模型装入较少数量的芯片，扩展到更多芯片可以简单地为我们提供更多的 FLOPs/s。例如，在推理期间，我们有时可以装入更小的拓扑结构，但选择扩展到更大的拓扑结构以减少延迟。同样，在训练期间，我们经常扩展到更多的芯片以减少步长时间。[↩]
GPU AllGather 也可以这样工作，你可以在一个节点中的 GPU 之间创建一个环，并按那个（任意）顺序传递数据块。[↩]
分子中的因子 2 来自于我们使用的是双向带宽。我们在每个方向发送 $V / X$，总共是 $2V / X$。[↩]
技术上是 $\lceil X / 2 \rceil$[↩]
对于偶数大小的双向环，每个设备将向右发送 $(N/2 + (N/2-1) + \ldots + 1)$ 个块，向左发送 $((N/2-1) + \ldots + 1)$ 个块 $= 0.5 \cdot (N / 2) \cdot (N/2 + 1) + 0.5 \cdot (N / 2) \cdot (N/2 - 1) = N^2/4$。每个块（即分片的分片）的大小是 $\text{bytes} / N^2$，所以每个设备的成本是 $(\text{bytes} / N^2) \cdot N^2 / 4 = \text{bytes} / 4$。这个结果在所有设备上都是可扩展的，因为总带宽随设备数量而扩展。[↩]

杂项

^*在 Google DeepMind 完成的工作，现就职于 MatX。

引用

在学术场合引用，请按如下格式引用本作品：

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

或使用 BibTeX 条目：

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }