例如，NVIDIA H100 每秒可执行约 9.89e14 次 bfloat16bf16 是 bfloat16 的缩写，这是一种在机器学习中常用的 16 位浮点格式。 FLOPs，而 TPU v6e 每秒可执行 9.1e14 次 FLOPs。H100 和 B200 通常只能达到声称的峰值 FLOPs 的 80-85% 左右，而 TPU 在正常使用中可以接近 95%。这意味着在 H100 上执行 1e12 FLOPs 大约需要 1e12 / 9.89e14 = 1.01ms，在 TPU v6e 上则需要 1e12 / 9.1e14 = 1.1ms。请注意，这些芯片的定价不同，此比较未按成本进行归一化。

芯片内通信： 在加速器内部，张量需要在片上内存（HBM）和计算核心之间传输。你会看到这个链接的带宽被称为“HBM 带宽”NVIDIA 也称之为“内存带宽”。。在 H100 上，这个值约为 3.35TB/s，而在 TPU v6e 上约为 1.6TB/s。

芯片间通信： 当我们将模型分布在多个加速器上时，张量需要频繁地在它们之间传输。我们的硬件上通常有几种选择（ICI、DCN 和 PCIe），每种选择都有不同的带宽。

无论是芯片内通信还是芯片间通信，我们都以字节/秒为单位来衡量，并用以下公式估算总通信时间：

\begin{matrix} (2) & T_{comms} = \frac{Communication Bytes}{Network/Memory Bandwidth Bytes/s} \end{matrix}

通常情况下（但并非总是如此），单个芯片内的计算可以与芯片内和芯片间的通信重叠。这意味着我们可以通过计算时间和通信时间的最大值来确定训练和推理时间的下限。我们也可以用它们的和来确定上限。在实践中，我们针对最大值进行优化，因为代数运算更简单，而且通过重叠通信和计算，我们通常可以接近这个下限。如果我们以最大值为目标进行优化，那么下限和上限的差异最多为 2 倍，因为 $T_\text{math} + T_\text{comms} \leq 2 * \max(T_\text{math}, T_\text{comms})$。然后，我们通过对“重叠区域”和开销进行建模来提高准确性，这可以通过分析特定模型和目标系统来获得信息。

\begin{matrix} (3) & T_{lower} = max (T_{math}, T_{comms}) \end{matrix}

\begin{matrix} (4) & T_{upper} = T_{math} + T_{comms} \end{matrix}

如果我们假设可以完美地重叠通信和计算，当 $T_\text{math} > T_\text{comms}$ 时，我们的硬件将得到充分利用。我们称之为“计算受限”（compute-bound）。当 $T_\text{comms} > T_\text{math}$ 时，我们往往是“通信受限”（communication-bound），并且至少有一部分加速器的 FLOPs/s 会因为等待数据传输而被浪费。判断一个操作是计算受限还是通信受限的一种方法是看它的“算术强度”（arithmetic intensity）或“操作强度”（operational intensity）。

定义： 算法的算术强度是指其执行的总 FLOPs 与其需要通信的字节数（无论是芯片内还是芯片间）之比。

\begin{matrix} (5) & Arithmetic Intensity = \frac{Computation FLOPs}{Communication Bytes} \end{matrix}

算术强度衡量的是给定操作的“每字节 FLOPs”。作为一阶近似，当我们的算术强度高时，$T_\text{math}$ 相对于 $T_\text{comms}$ 较大，我们通常会使用大部分可用的 FLOPs。当情况相反时，我们会在通信上花费更多时间并浪费 FLOPs。发生交叉的点是我们硬件的“峰值算术强度”，即峰值加速器 FLOPs/s 与加速器带宽之比。

\begin{aligned} T_{math} > T_{comms} \Leftrightarrow \frac{Computation FLOPs}{Accelerator FLOPs/s} > \frac{Communication Bytes}{Bandwidth Bytes/s} \\ \Leftrightarrow \frac{Computation FLOPs}{Communication Bytes} > \frac{Accelerator FLOPs/s}{Bandwidth Bytes/s} \\ \Leftrightarrow Intensity (Computation) > Intensity (Accelerator) \end{aligned}

$\text{Intensity}(\text{Accelerator})$ 是我们的加速器达到其峰值 FLOPs/s 时的算术强度。对于 TPU v5e MXU，这个值约为 240 FLOPs/字节MXU 是 TPU 上的矩阵乘法单元。我们在这里特别指出，是因为 TPU 还有其他加速器，如 VPU，它负责元素级运算，具有不同的峰值 FLOPs/s。，因为 TPU 每秒可执行 1.97e14 FLOPs 并从 HBM 加载 8.2e11 字节/秒。这意味着如果一个算法的算术强度低于 240这仅在算法从 HBM 加载权重并在 MXU 中运行时才成立。正如我们将在下一节讨论的，我们有时可以将参数存储在具有更高带宽的 VMEM 中。许多算法也在 VPU 中运行，它具有不同的性能特征。 FLOPs/字节，它将受到字节加载的限制，因此我们无法充分利用硬件。让我们来看一个这样的例子：

示例（点积）: 为了计算两个 bfloat16 精度向量的点积，x • y: bf16[N], bf16[N] → bf16[1]，我们需要从内存中加载 $x$ 和 $y$，每个向量有 $2 * N = 2N$ 字节，执行 $N$ 次乘法和 $N-1$ 次加法，并将 2 字节写回 HBM $\begin{matrix} (6) & Intensity (dot product) = \frac{Total FLOPs}{Total Bytes} = \frac{N + N - 1}{2 N + 2 N + 2} = \frac{2 N - 1}{4 N + 2} \to \frac{1}{2} \end{matrix}$

当 $N\rightarrow\infty$ 时。所以点积的算术强度为 $\frac{1}{2}$，换句话说，点积每加载一个字节执行 0.5 次浮点运算。这意味着我们的算术强度低于硬件的算术强度，因此我们将是通信受限的。上面 240 这个数字在这里不是一个正确的比较，因为正如你将在下一节中看到的，点积是在 VPU 而非 MXU 上执行的。TPU v5p VPU 每秒大约可以执行 7e12 FLOPs，所以它的临界强度大约是 3，这意味着我们在这里仍然有些通信受限。无论如何，我们的强度低且恒定这一事实意味着在大多数硬件上很难达到计算受限。

可视化Roofline模型

我们可以使用Roofline图来可视化内存和计算之间的权衡。Roofline图绘制了算法在我们的硬件上可实现的峰值 FLOPs/s（吞吐量）（y 轴）与该算法的算术强度（x 轴）之间的关系。这是一个对数-对数图的例子：

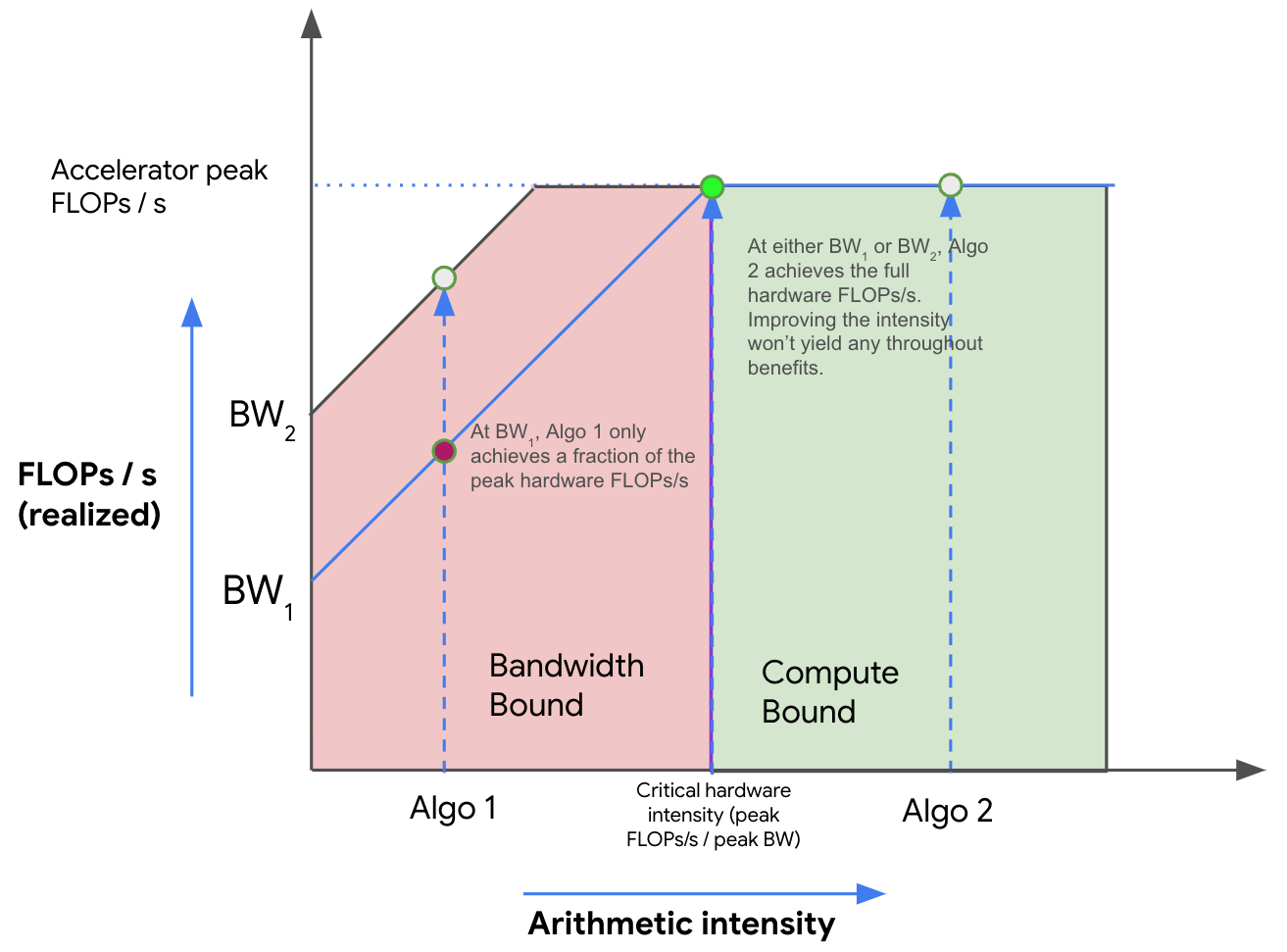
图：一个Roofline图示例，展示了两个具有不同算术强度的算法（算法 1 和算法 2）及其在不同带宽（BW1 和 BW2）下对应的理论峰值吞吐量。在红色区域，算法在两种带宽下都受到带宽限制，并且浪费了硬件峰值 FLOPs/s 的一部分。黄色区域仅在较低带宽（BW1）下受到带宽限制。绿色区域在所有带宽下都受到计算限制。在这里，我们正在使用加速器的峰值 FLOPs/s，增加带宽或提高强度不会带来任何好处。

上图中，随着强度增加（从左到右），我们最初看到算法性能（以 FLOPs/s 为单位）呈线性增长，直到达到硬件的临界算术强度，对于 TPU v5e 来说是 240。任何强度较低的算法都将受到带宽（BW）限制，并受限于峰值内存带宽（红色区域所示）。任何在右侧的算法都将充分利用我们的 FLOPs（绿色区域所示）。在这里，算法 1 是通信受限的，只使用了总硬件 FLOPs/s 的一部分。算法 2 是计算受限的。我们通常可以通过增加算法的算术强度或增加可用内存带宽（从 BW1 移动到 BW2）来提高算法的性能。

矩阵乘法

让我们来看看我们即将最喜欢的算法：矩阵乘法（也称为 matmul）。我们写成 $X * Y \rightarrow Z$，其中 $X$ 的形状为 $\text{bf16}[B, D]$，$Y$ 的形状为 $\text{bf16}[D, F]$，而 $Z$ 的形状为 $\text{bf16}[B, F]$。为了进行矩阵乘法，我们需要加载 $2DF + 2BD$ 字节，执行 $2BDF$ FLOPs，并写回 $2BF$ 字节。技术上我们执行 $BF \times (2D - 1)$ FLOPs，但这已经足够接近了。这来自于 $BDF$ 次乘法和 $BF * (D-1)$ 次加法。第 4 节有更多细节。虽然矩阵乘法的输出技术上是 float32，但我们通常在复制回 HBM 之前将其转换为 bfloat16。因此：

\begin{matrix} (7) & Intensity (matmul) = \frac{2 B D F}{2 B D + 2 D F + 2 B F} = \frac{B D F}{B D + D F + B F} \end{matrix}

如果我们假设“批次大小”$B$ 相对于 $D$ 和 $F$ 较小，我们可以得到一个很好的简化。那么我们得到

\begin{matrix} (8) & \frac{B D F}{B D + D F + B F} ≊ \frac{B D F}{D F} = B \end{matrix}

\begin{matrix} (9) & Intensity (matmul) > Intensity (TPU) ⟹ B > \frac{1.97 e 14}{8.20 e 11} = 240 \end{matrix}

对于 Transformer 的矩阵乘法来说，这是一个合理的假设，因为我们通常有一个本地（每个副本）的批次大小 $B < 1024$ 个 token（不是序列），但 $D$ 和 $F > 8000$。因此，当我们的每个副本我们说“每个副本”，是因为如果我们进行某种模型分片来增加矩阵乘法中使用的芯片数量，我们会将可用的计算和内存带宽按相同比例进行扩展。因此，临界批次大小是针对模型权重的每个独立副本而言的。的批次大小大于 240 个 token 时，我们通常会变得计算受限，这是一个非常简单的规则！

要点： 对于 bfloat16 矩阵乘法，要在大多数 TPU 上达到计算受限，我们的每个副本的 token 批次大小需要大于 240。请注意，这不是通常意义上的批次大小，即序列的批次大小。事实证明，大多数Roofline模型纯粹取决于 token 的数量，无论它们是属于相同还是不同的序列。例如，如果你在 128 个 GPU 上有一个批次大小为 512 个序列，每个序列 4096 个 token，那么你的总批次大小为 `512 * 4096 = 2M` 个 token，本地批次大小为 16k 个 token。

这有一些值得注意的警告，我们将在下面的问题中探讨，特别是关于量化（例如，如果我们量化我们的激活但仍然进行全精度 FLOPs），但这是一个值得记住的好规则。对于 GPU，这个数字略高（接近 300），但同样的结论通常成立。当我们将一个大的矩阵乘法分解成更小的矩阵乘法时，分块的大小也很重要。当我们进行一个大的矩阵乘法时，我们需要将其分解成更小的分块，以适应 VMEM/SMEM/TMEM 这种更高带宽的片上内存。这导致我们需要多次加载数据块，所以我们只加载 $O(N^2)$ 字节的说法不再完全正确。考虑一个 $(m, k) \cdot (k, n)$ 的矩阵乘法，其分块大小为 $bm, bk, bm$。令 $tm = m / bm$，等等。那么总 FLOPs 是 $2 \cdot tm \cdot tn \cdot tk \cdot m \cdot bk \cdot bm$，总字节数是 $2 \cdot tm \cdot tn \cdot (tk \cdot (bm \cdot bk + bk \cdot bn) + 2 \cdot bm \cdot bn)$。忽略最后一项，我们得到的强度是 $bm \cdot bn / (bm + bn)$，这与上面的类似。我们将在下一节中讨论更底层的 GPU 和 TPU 细节。

网络通信Roofline模型

到目前为止，我们讨论的所有Roofline模型都是内存带宽Roofline模型，全部在单个芯片内部。这不应被视为一个规则。事实上，本书中我们关心的多数Roofline模型都涉及芯片间的通信：通常是涉及跨多个 TPU 分片的矩阵的矩阵乘法。

举一个有点刻意的例子，假设我们想将两个大矩阵 $X\sim \text{bfloat16[B, D]}$ 和 $Y \sim \text{bfloat16[D, F]}$ 相乘，这两个矩阵均匀地分布在 2 个 TPU/GPU 上（沿着 $D$ 维度）。要进行这次乘法（我们将在第 3 节中看到），我们可以在每个 TPU 上乘以每个矩阵的一半（在 TPU 0 上是 A = X[:, :D // 2] @ Y[:D // 2, :]，在 TPU 1 上是 B = X[:, D // 2:] @ Y[D // 2:, :]），然后将得到的“部分和”复制到另一个 TPU 上并相加。假设我们可以在每个方向上复制 4.5e10 字节，并在每个芯片上执行 1.97e14 FLOPs/s。那么 $T_\text{math}$ 和 $T_\text{comms}$ 是多少？

$T_\text{math}$ 显然是之前的一半，因为每个 TPU 只做了一半的工作，即我们忽略了将两个部分和相加所需的 FLOPs（另外 DF 次加法），但这基本上可以忽略不计。

T_{math} = \frac{2 B D F}{2 \cdot Accelerator FLOPs/s} = \frac{B D F}{1.97 e 14}

那么 $T_\text{comms}$ 呢？这现在指的是芯片间的通信时间！它就是发送的总字节数除以网络带宽，即

T_{comms} = \frac{2 B F}{Network Bandwidth} = \frac{2 B F}{4.5 e 10}

因此，当 $Intensity (matmul (2-chips)) > Intensity (TPU w.r.t. inter-chip network)$ 或者等价地当 $\frac{BDF}{2BF} = \frac{D}{2} > \frac{1.97e14}{4.5e10} = 4377$ 或者 $D > 8755$ 时，我们变得计算受限（现在是相对于芯片间网络）。请注意，与之前不同，临界阈值现在取决于 $D$ 而不是 $B$！试着思考一下为什么。这只是一个例子，但我们想强调，这种Roofline模型对于了解何时可以在多个 TPU 之间并行化一个操作至关重要。

几个练习题

问题 1 [int8 矩阵乘法]： 假设我们想用 int8 精度（每个参数 1 字节）而不是 bfloat16 来进行矩阵乘法 $X[B, D] \cdot_D Y[D, F] \rightarrow Z[B, F]$。在本文中，我们将使用符号 $A \cdot_D B$ 来表示乘法正在对 D 维度进行收缩。这是对 einsum 符号的一种滥用。

需要从内存加载多少字节？需要写回内存多少字节？
总共执行了多少次操作（OPs）？
算术强度是多少？
$T_\text{math}$ 和 $T_\text{comms}$ 的Roofline估计值是多少？整个操作运行时间的合理上限和下限是什么？

假设我们的 HBM 带宽是 8.1e11 字节/秒，我们的 int8 峰值 OPs/s 是 3.94e14（大约是 bfloat16 的 2 倍）。

点击这里查看答案。

因为我们用 int8 存储参数，每个参数占 1 字节，所以我们从 HBM 加载了 $B D + D F$ 字节，并写回了 $B F$ 字节。
这和 bfloat16 的情况一样，但理论上 int8 OPs/s 应该更快。所以这仍然是 $2BDF$ FLOPs。
算术强度是 $2 B D F / (B D + D F + B F)$ 。如果我们像上面一样对 $B ≪ D$ 和 $B ≪ F$ 作出相同的假设，我们得到的算术强度是 $2 B$ ，这意味着我们的规则变成了 $B > \text{HBM int8 算术强度} / 2$。使用给定的数字，这个 int8 强度是 3.94e14 / 8.1e11 = 486，所以规则是 $B > 486 / 2 = 243$。注意，这基本上没变！
$T_{math} = 2 B D F / 3.94 e 14$ 和 $T_{comms} = (B D + D F + B F) / 8.1 e 11$ ，所以一个合理的下限是 $max (T_{math}, T_{comms})$ ，一个上限是 $T_{math} + T_{comms}$ 。

问题 2 [int8 + bf16 矩阵乘法]： 在实践中，我们经常对权重和激活进行不同的量化，所以我们可能会用非常低的精度存储权重，但保持激活（和计算）在较高的精度。假设我们想用 int8 量化权重，但保持激活（和计算）在 bfloat16。在什么批次大小时我们会变得计算受限？假设 1.97e14 bfloat16 FLOPs/s。

提示：这具体指的是 bfloat16[B, D] * int8[D, F] -> bfloat16[B, F]，其中 $B$ 是“批次大小”。

点击这里查看答案。

再次假设 B 很小，我们有 2BDF bfloat16 FLOPs，但只有 DF 的权重（而不是 bfloat16 中的 2DF）。这意味着当 $2 B > 240$ 或 $B > 120$ 时，我们变得计算受限。这个值低得多，意味着如果我们能做 int8 权重量化（这相当容易做到）但仍然执行 bfloat16 FLOPs，我们将在效率上获得有意义的提升（尽管 int8 OPs 会更好）。

问题 3： 沿用问题 2 的设置，绘制当 $F = D = 4096$ 和 $F = D = 1024$ 时，峰值 FLOPs 与 $B$ 的Roofline图。使用加载的确切字节数，而不是近似值。

点击这里查看答案。

这是所说的图：

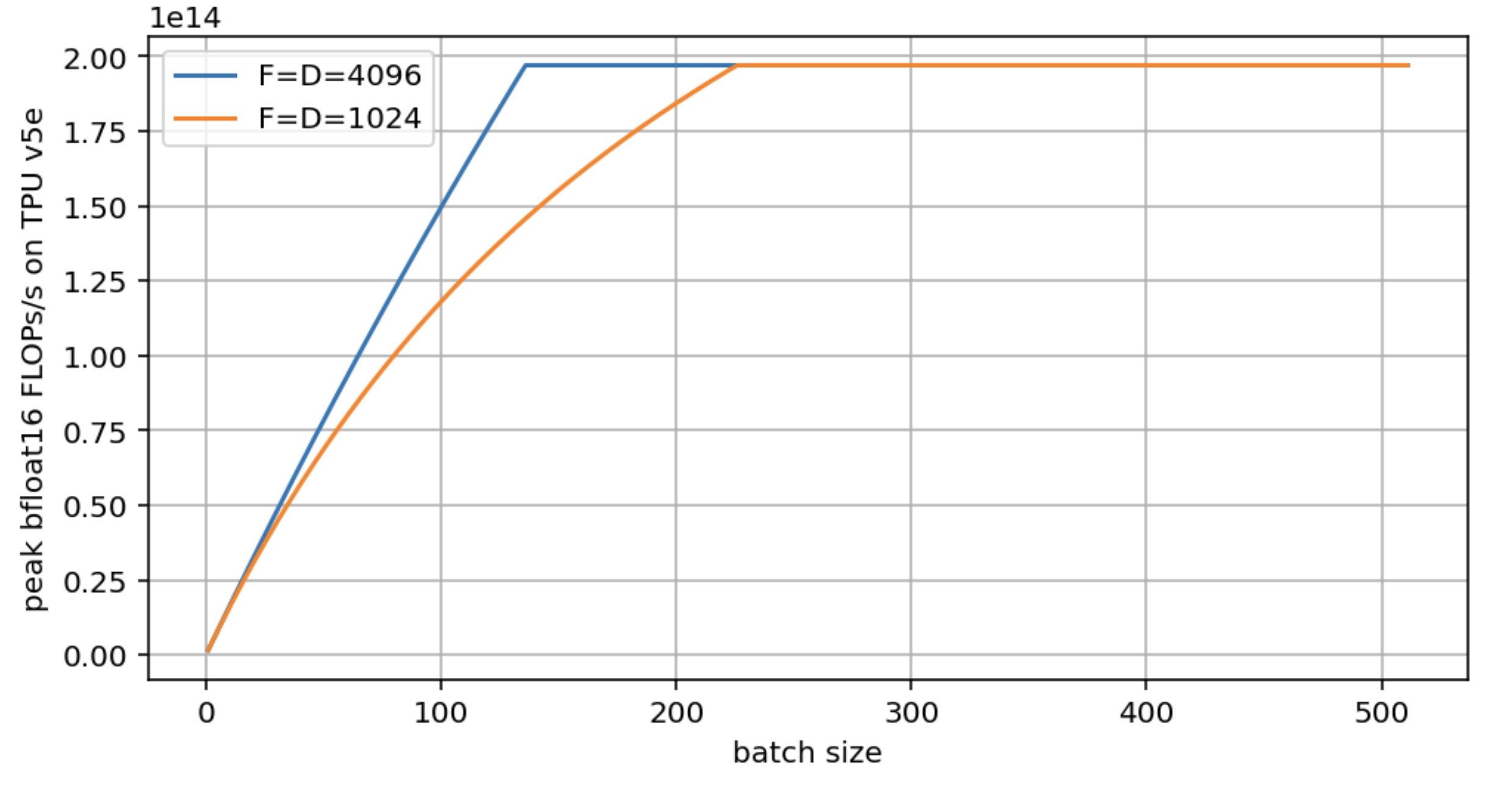
请注意，两个模型最终都达到了硬件的峰值 FLOPs/s，但较大的 D/F 更早达到。D=F=1024 几乎使临界批次大小翻倍。生成此图的代码在这里：

import matplotlib.pyplot as plt
import numpy as np

bs = np.arange(1, 512)

def roofline(B, D, F):
  total_flops = 2*B*D*F
  flops_time = total_flops / 1.97e14
  comms_time = (2*B*D + D*F + 2*B*F) / 8.2e11
  total_time = np.maximum(flops_time, comms_time)
  return total_flops / total_time

roofline_big = roofline(bs, 4096, 4096)
roofline_small = roofline(bs, 1024, 1024)

plt.figure(figsize=(8, 4))
plt.plot(bs, roofline_big, label='F=D=4096')
plt.plot(bs, roofline_small, label='F=D=1024')
plt.legend()
plt.xlabel('batch size')
plt.ylabel('peak bfloat16 FLOPs/s on TPU v5e')
plt.grid()

问题 4： 如果我们想执行 $\text{int8[B, D]} *_D \text{int8[B, D, F]} \rightarrow \text{int8[B, F]}$，其中我们想象每个批次元素都有一个不同的矩阵。这个操作的算术强度是多少？

点击这里查看答案。

让我们先看看总的 FLOPs 和通信量。

总 FLOPs：FLOPs 基本上是相同的，因为我们正在做相同数量的 $B D \times D F$ 矩阵乘法（这在第 4 节中有更多讨论）。所以这只是 $2 B D F$ 。
总通信量：我们这里有更多的通信量： $B D + B D F + B F$ 。
因此，我们的算术强度现在实际上是 $2 B D F / (B D + B D F + B F)$ 。由于 $B D F$ 在分母中占主导地位，这大约是 $2$ 。所以它不再取决于批次大小，而是基本上是恒定的。这很糟糕，因为这意味着无论如何我们基本上总是会受到通信限制。

问题 5 [GPU 的内存Roofline模型]： 使用 NVIDIA 提供的 H100 规格表，计算矩阵乘法变得计算受限时的批次大小。请注意，TensorCore 的 FLOPs 数值是真实值的两倍，因为它们只有在结构化稀疏性的情况下才能实现。

点击这里查看答案。

从规格表中，我们看到报告的 bfloat16 FLOPs 值为 1.979e15 FLOPs/s，并带有一个星号注明“带稀疏性”。没有稀疏性的真实值是这个的一半，意味着接近 1e15 FLOPs/s。内存带宽是 3.35TB/s，即 3.35e12 字节/秒。因此 $B_\text{crit}$ 是 1e15 / 3.35e12 = 298，与 TPU 相当类似。

第 1 部分到此结束！要查看第 2 部分，了解真实 TPU 如何处理 FLOPs 和通信，请点击这里。

脚注

bf16 是 bfloat16 的缩写，这是一种在机器学习中常用的 16 位浮点格式。[↩]
H100 和 B200 通常只能达到声称的峰值 FLOPs 的 80-85% 左右，而 TPU 在正常使用中可以接近 95%。[↩]
请注意，这些芯片的定价不同，此比较未按成本进行归一化。[↩]
NVIDIA 也称之为“内存带宽”。[↩]
MXU 是 TPU 上的矩阵乘法单元。我们在这里特别指出，是因为 TPU 还有其他加速器，如 VPU，它负责元素级运算，具有不同的峰值 FLOPs/s。[↩]
这仅在算法从 HBM 加载权重并在 MXU 中运行时才成立。正如我们将在下一节讨论的，我们有时可以将参数存储在具有更高带宽的 VMEM 中。许多算法也在 VPU 中运行，它具有不同的性能特征。[↩]
上面 240 这个数字在这里不是一个正确的比较，因为正如你将在下一节中看到的，点积是在 VPU 而非 MXU 上执行的。TPU v5p VPU 每秒大约可以执行 7e12 FLOPs，所以它的临界强度大约是 3，这意味着我们在这里仍然有些通信受限。无论如何，我们的强度低且恒定这一事实意味着在大多数硬件上很难达到计算受限。[↩]
技术上我们执行 $BF \times (2D - 1)$ FLOPs，但这已经足够接近了。这来自于 $BDF$ 次乘法和 $BF * (D-1)$ 次加法。第 4 节有更多细节。[↩]
虽然矩阵乘法的输出技术上是 float32，但我们通常在复制回 HBM 之前将其转换为 bfloat16。[↩]
我们说“每个副本”，是因为如果我们进行某种模型分片来增加矩阵乘法中使用的芯片数量，我们会将可用的计算和内存带宽按相同比例进行扩展。因此，临界批次大小是针对模型权重的每个独立副本而言的。[↩]
请注意，这不是通常意义上的批次大小，即序列的批次大小。事实证明，大多数Roofline模型纯粹取决于 token 的数量，无论它们是属于相同还是不同的序列。例如，如果你在 128 个 GPU 上有一个批次大小为 512 个序列，每个序列 4096 个 token，那么你的总批次大小为 `512 * 4096 = 2M` 个 token，本地批次大小为 16k 个 token。[↩]
当我们进行一个大的矩阵乘法时，我们需要将其分解成更小的分块，以适应 VMEM/SMEM/TMEM 这种更高带宽的片上内存。这导致我们需要多次加载数据块，所以我们只加载 $O(N^2)$ 字节的说法不再完全正确。考虑一个 $(m, k) \cdot (k, n)$ 的矩阵乘法，其分块大小为 $bm, bk, bm$。令 $tm = m / bm$，等等。那么总 FLOPs 是 $2 \cdot tm \cdot tn \cdot tk \cdot m \cdot bk \cdot bm$，总字节数是 $2 \cdot tm \cdot tn \cdot (tk \cdot (bm \cdot bk + bk \cdot bn) + 2 \cdot bm \cdot bn)$。忽略最后一项，我们得到的强度是 $bm \cdot bn / (bm + bn)$，这与上面的类似。[↩]
我们忽略了将两个部分和相加所需的 FLOPs（另外 DF 次加法），但这基本上可以忽略不计。[↩]
在本文中，我们将使用符号 $A \cdot_D B$ 来表示乘法正在对 D 维度进行收缩。这是对 einsum 符号的一种滥用。[↩]

杂项

^*工作于 Google DeepMind 完成，现就职于 MatX。

引用

在学术背景下进行归属时，请按如下方式引用本作品：

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

或作为 BibTeX 条目：

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }